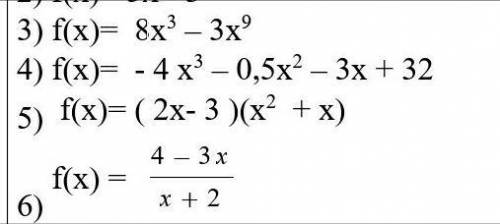
Коротко: Наша цель найти k и b, чтобы подставить их в уравнение прямой y = kx + b.
Подробное решение:
Рассмотрим 1ую функцию:Возьмем произвольную точку; пусть это будет точка A(0; 0). Мы видим по графику, что это прямая. Уравнение прямой: y = kx + b (в некоторых учебниках пишут y = kx + m разницы нет вообще (только буква другая) ).
Мы смотрим, какой x у точки A (т.е. на 1ое число после скобки A(x; y) ). Видим, что x = 0. Аналогично и y = 0. Подставим эти значения в формулу. Вместо y (в формуле y = kx + b) идет 0; вместо x тоже 0, но его мы уже подставляем суда: y = kx + b. Получим: 0 = 0 + b. Это простейшее линейное уравнение. Хорошо видно, что b = 0.
Отлично, b нашли. Теперь найдем k. Возьмем любую другую точку, где x не равен 0. Пусть это будет точка B(2; 1). Помнишь как найти x и y этой точки? Правильно: x = 2, y = 1 (т.к. B(x; y) ). Подставим их в уравнение прямой y = kx + b (мы не забываем про b, его мы уже знаем). Получили: 1 = k * 2 + 0. Простое линейное уравнение. Решив его, увидим, что k = 0.5.
Теперь подставим k и b в наше уравнение прямой. Результатом всех наших действий стала формула уравнения прямой 1ой функции. ответ на 1ую задачу: y = 0.5x
Рассмотрим 2ую функцию:Я бы сказал, она самая простая. Y здесь фиксированный и не меняется при изменении x! Поэтому в таких случаях мы просто пишем y = 2. Эта функция всегда дает нам значение 2. Применять алгоритм из 1ого примера ни в коем случае не нужно.
Рассмотрим 3ью функцию:Применим алгоритм из 1ого примера. Возьмем точку A(0; 3). 3 = 0 + b => b = 3. Возьмем точку B(2; 0). 0 = 2 * k + 3 => k = -1.5. Все просто! ответ: y = -1.5k + 3
max {k / S(k)} = 1 000 000
Объяснение:
Цифра в старшем разряде не может быть равна 0, потому что в противном случае число не будет семизначным. Сначала рассмотрим случай, когда это единственная ненулевая цифра в числе k:
Теперь предположим, что в числе есть другие ненулевые цифры и покажем, что в этом случае значение дроби меньше 10⁶. Цифры числа k обозначим через a₆, a₅, ..., a₀.
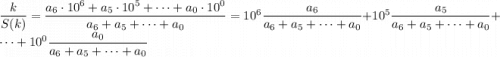
Рассмотрим дробь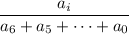 
, где 
– одна из цифр числа k. Заметим, что 
для любых x>0 и y≥0. Тогда если мы оставим в знаменателе этой дроби только два слагаемых, одно из которых (ai) присутствует в числителе, а второе (aj) не равно нулю, будет верно неравенство:
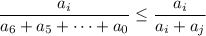
Если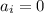 
, то 
. В противном случае мы можем поделить числитель и знаменатель дроби на : 
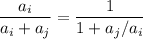, а поскольку ai и aj – это некоторые отличные от нуля цифры, максимально возможное значение этой дроби достигается при ai=9 и aj=1: 
.
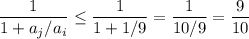Из этого следует, что 
.
Теперь вернемся к исходному отношению k/S(k) при наличии хотя бы двух отличных от нуля цифр:
Таким образом, мы доказали, что максимальное значение дроби k/S(k) равно 10⁶ = 1000000 и достигается, когда все все цифры числа k, кроме первой, равны нулю.
ответ смотрите на фото.