тут собрался коктейль формул косинуса разности и суммы, формулы синуса разности и суммы.
cos(α-β)=cosαcosβ+sinαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
а) cos(5П/8)*cos(3П/8)+sin(5П/8)*sin(3П/8)=cos(5π/8-3π/8)=cos(2π/8)=cos(π/4)=1/√2
б) sin(2П/15)*cos(П/5)+cos(2П/15)*sin(П/5)=
=sin(2π/15+π/5)=sin(π/3)=√3/2
в) cos(П/12)*cos(П/4)-sin(П/12)*sin(П/4)=cos(π/12+π/4)=cos(π/3)=1/2
г) sin(П/12)*cos(П/4)-cos(П/12)*sin(П/4)
=sin(π/12-π/4)=sin(11π/6)=-1/2
========================================================
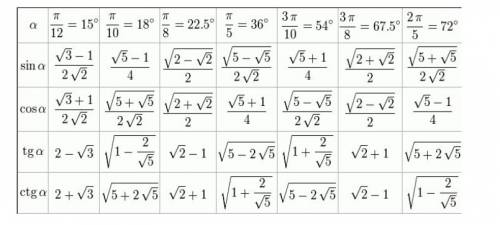
таблица нестандартных углов смотри во вложении!
Существуют условия чётности/нечётности функции.
Если f(-x) = f(x) - функция чётная.
Если f(-x) = -f(x) - функция нечётная.
В противном случае говорят, что функция не обладает чётностью.
Теперь исследуем на чётность наши функции.
1)f(-x) = 3(-x)² - cos(-x) = 3x² - cos x = f(x) - функция чётная
2)f(-x) = sin(-2x) + (-x)³ = -sin 2x - x³ = -(sin 2x + x³) = -f(x) - функция нечётная
3)f(-x) = 2(-x)⁴ + cos(-x) = 2x⁴ + cos x = f(x) - функция чётная
4)g(-x) = tg(-x) - 4(-x)⁵ = -tg x + 4x⁵ = -(tg x - 4x⁵) = -g(x) - функция нечётная
5)Не очень понял, что вы имели в виду
6)Здесь, если я не ошибаюсь, речь идёт о функции f(x) = 2x³ / (cos x - 1). Тогда,
f(-x) = 2(-x)³ / (cos(-x) - 1) = -2x³ / (cos x - 1) = -f(x) - функция нечётная