{у=х+5
{Х×у=36
Х×(Х+5)=36
Х^2+5Х=36
Х^2+5Х-36=0
D=5^2-4×1×(-36)=25+144=169
X1=(-5-13)/2= - 9
X2=(-5+13)/2=4
y1= - 9+5= - 4
y2= 4+5=9
Проверка :
(-9;-4)
{-4= - 9+5
{-9×(-4)=36
{-4= - 4
{36=36
(4;9)
{9=4+5
{4×9=36
{9=9
{36=36
ответ : ( - 9; - 4) (4; 9)
Число под логарифмом должно быть строго положительно.
Если дробь равна 0, то числитель равен 0, а знаменатель не равен 0.
Область определения:
{ sin x > 0; x ∈ (2pi*k; pi+2pi*k)
{ cos x ≠ -√3/2; x ≠ 5pi/6 + 2pi*k; x ≠ 7pi/6 + 2pi*k
ОДЗ: x ∈ (2pi*k; 5pi/6 + 2pi*k) U (5pi/6 + 2pi*k; pi + 2pi*k)
Решаем уравнение
1)
sin x = 1
x1 = pi/2 + 2pi*k
2)
sin x = 1/2
x2 = pi/6 + 2pi*k
x3 = 5pi/6 + 2pi*k - не подходит
ответ: x1 = pi/2 + 2pi*k; x2 = pi/6 + 2pi*k
На промежутке [0; 3pi/2] будут корни x1 = pi/6; x2 = pi/2
раскроем модуль по определению:
для у < 0: -у = |x^2 + 4x|
для у ≥ 0: у = |x^2 + 4x|
теперь про икс... для икс два корня: (-4) и (0)---три промежутка
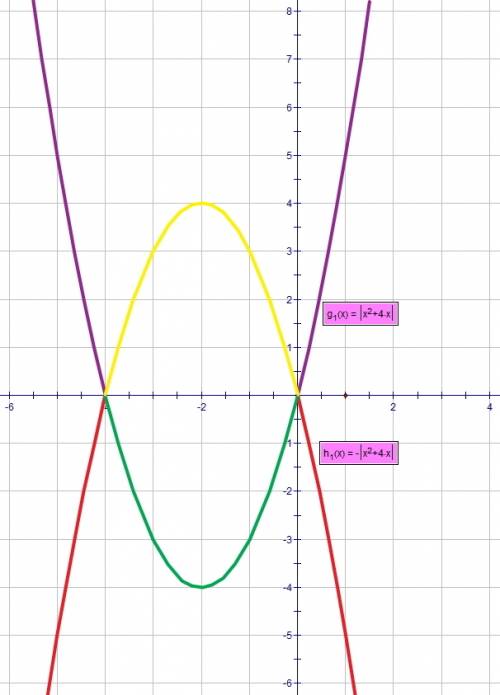
для у < 0 и х ∈ (-∞;-4]U[0;+∞) т.е. под модулем выражение НЕотрицательное : -у = x^2 + 4x ---> y = -x^2 - 4x (красный цвет)
для у < 0 и х ∈ (-4;0) т.е. под модулем выражение отрицательное : -у = -x^2 - 4x ---> y = x^2 + 4x (зеленый цвет)
для у ≥ 0 и х ∈ (-∞;-4]U[0;+∞) т.е. под модулем выражение НЕотрицательное : у = x^2 + 4x (фиолетовый цвет)
для у ≥ 0 и х ∈ (-4;0) т.е. под модулем выражение отрицательное : y = -x^2 - 4x (желтый цвет) и все вместе--это график данного уравнения...
y=x+5
x*y=36
x*(x+5)=36
x²+5x=36
x²+5x-36=0
получаем уравнение вида:
ax²+bx+c=0
ищем дискриминант:
D=b²-4ab
D=5²-4*(-36)*1=25+144=169
корни х1 и х2 по формуле:
подставляем значения х к у:
y1=4+5=9
y2=-9+5=4
проверяем:
y1*x1=9*4=36
y2*x2=-9*4=-36 (ложные)
ответ: х=4, у=9