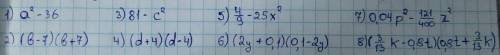
Объяснение:
2.
a) 3x+12>4x-1 | (-x>-13) /-1 | x<13
7-2x<=10-3x | -3 <= -x /-1 | x <= 13. x принадлежит (-∞; 13].
б) 2x-9 > 6x+1 | (-4x > 10) / -4 | x<10
( -
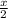< 2 ) *-2 | x > 4. x принадлежит (-∞; 10) и (4; +∞).
3.
а)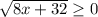 
Взводим все в квадрат
8x+32 => 0
8x => 32 делим все на 8
x => 4. x принадлежит [4; +∞).
б)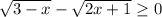 
Взводим все в квадрат
3-x-2x+1 => 0
4 => 3x Делим все на 3
1.3 => x
x <= 1.3. x принадлежит [-∞; 1.3).
4.
а-7 => 0 3-2a => 0
a => 7 3 => 2a
1.5 => a ответ: a принадлежит [7; +∞).
Можно сделать графически.
Левая часть: y = -0,5x⁴
График - квадратичная парабола, ветви направлены вниз.
Правая часть: y = x - 4
График - прямая линия, не параллельная осям координат. Пересекает параболу в двух точках.
ответ: уравнение имеет 2 действительных корня.
2) y=(x-2)^2+4 на отрезке [0;3]
Квадратичная функция, ветви направлены вверх. Наименьшим значением будет вершина параболы.
Координаты вершины параболы: х=2 (из уравнения функции), у = 4.
Подставить границы интервала в уравнение функции и выбрать наибольшее:
y = (x - 2)² + 4 = (0 - 2)² + 4 = 8
y = (x - 2)² + 4 = (3 - 2)² + 4 = 5
Наибольшее значение функции на отрезке [0; 3] y = 8 в точке x = 3.
Наименьшее значение функции на отрезке [0; 3] y = 4 в точке x = 2.