
Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Значит, 1/x - производительность первого насоса до ремонта, а 1/y - производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1
1,2(1/x) - производительность первого насоса до ремонта, а 1,6(1/y) - производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
ответ: 10 ч.
Поставь лучший ответ
1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
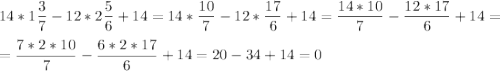
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
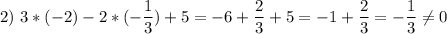
не является решением
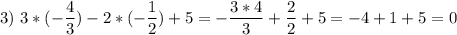
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
Сумма частот равна количеству элементов в выборке
Выборка: 70 учащихся
Сумма частот равна: 70=1+2+4+5+х+12+8+6+3=41+х
х=70-41
х=29
ответ: пропущенное значение частоты - 29