____________________________________________________________________________________________________________________________
![выбери верные утдверждения о функции y=0,5x^2-4 Верных ответов: 5 промежуток убывания x ∈ (–∞; 0] гр](/tpl/images/2112/5120/e2ef0.jpg)
Объяснение:
Данная функция 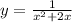 — дробно-рациональная функция.
— дробно-рациональная функция.
Областью определения такой функции будет всё множество чисел, за исключением таких, которые обращают знаменатель в ноль, так как на ноль делить нельзя — в такой точке функция будет не определена.
Таким образом, следует найти все числа, обращающие знаменатель дроби в ноль, и исключить их из области определения.
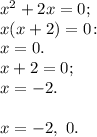
Функция имеет две точки, где она не определена, поэтому областью определения будет объединение трёх интервалов, исключающих эти точки.
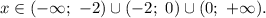
ответом будет полученное числовое множество.
 и
и 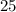 – среднеарифметическое равно
– среднеарифметическое равно 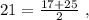 и при этом
и при этом  на
на 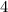 меньше двадцати пяти и на
меньше двадцати пяти и на 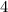 больше семнадцати.
больше семнадцати.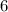 монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на 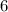 монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на 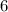 монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на 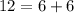 монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.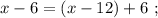
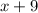 монет, а у Пети-II будет
монет, а у Пети-II будет 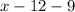 монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в 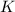 раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 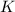 раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение: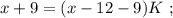


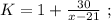
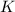 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 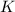 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда  откуда:
откуда: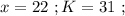
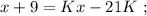
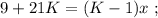
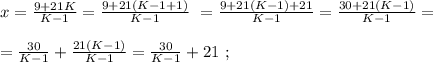

 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет  откуда:
откуда: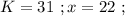
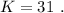
1)область определения функции (–∞; +∞)
2)прямая x = 0 является осью симметрии графика функции
3)промежуток убывания x ∈ (–∞; 0]
4)график функции проходит через точку (2; –2)
5)вершина параболы – точка (0; –4).
Объяснение:Вот ответ, если не правельно то любить и жаловать.