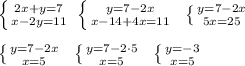
Если так не видишь,что эти уравнения похожи на обычные квадратные, то сделай замену х^2=t
а) х^4-3х^2+2=0 сделаем замену и получим:
t^2-3t+2=0, дальше по теореме Виетта ищем корни, которые видны сразу:
t=2
t=1 , дальше возвращаемся к изначальным переменным:
х^2=2
х^2=1, отсюда:
х=корень из 2
х=минус корень из 2
х=1
х=-1
Я думаю ты поняла и поэтому я опустила моменты с заменами. Если непонятно спрашивай
б)х^4-10х^2+9=0
х^2=9
х^2=1
ответ:х=3
х=-3
х=1
х=-1
в)х^4-5х^2+4=0
х^2=4
х^2=1
ответ:х=2
х=-2
х=-1
х=1
г)х^4-26х^2+25=0
х^2=25
х^2=1
ответ:х=5
х=-5
х=1
х=-1
д)х^4-20х^2+64=0
х^2=16
х^2=4
ОТвет:х=4
х=-4
х=2
х=-2
Координаты точек пересечения (0; 0) (-3; 16,2)
Объяснение:
Определи координаты точек пересечения графиков функций
y=x²−2,4x y= −5,4x.
Первый график - парабола, второй - прямая линия.
1)Приравняем правые части уравнений (левые равны) и вычислим х:
х²-2,4х= -5,4х
х²-2,4х+5,4х=0
х²+3х=0 неполное квадратное уравнение
х(х+3)=0
х₁=0
х+3=0
х₂= -3
При значений х вычислить значения у:
y= −5,4x
у₁= -5,4*0
у₁=0
у₂= -5,4*(-3)
у₂=16,2
Как видно из вычислений, график прямой линии у -5,4х пересекает параболу y=x²−2,4x в двух точках.
Координаты точек пересечения (0; 0) (-3; 16,2)