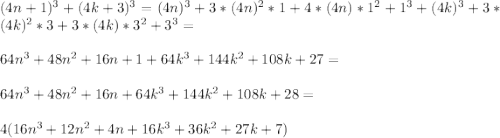
Объяснение:
коэффициент х3 при классификации биномов (2 x) 4.
[2]
2. Нарисуйте множество точек, которые являются решением системы неравенств:
x2 y2 ≤ 9,
x2 y2 6x 0.
x2 ≥ y2-4х ≥ 0,
[3]
3.Решите систему уравнений:
a b 6,
a2 b2 20.
[4]
4. периметр прямоугольника равен 18 см, а сумма площадей квадратов, вложенных в его соседние стенки, равна 41 см2. Найдите стенки прямоугольника.
[3]
5. без повторения цифр в составе числа, 1, 2, 3, 4, 5 сколько трехзначных чисел можно составить без остатка, делящихся на 2, образованных цифрами?
[3]
6. в коробке 3 желтых и 5 синих шарика.
а) сколько можно выбрать из коробки 3 шарика?
в) сколько выбрать хотя бы 2 желтых шара из 4-х выбранных из коробки?
Т=Период тригонометрической функции / к, где к-коэффициент перед х в функции
Период тангенса Пи, к=6, значит наименьший положительный период равен Пи/6