решить задачи по алгебре . 1. Периметр прямоугольника равен 62 м. Найдите его стороны, если площадь прямоугольника равна 210 м2.
2. Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 см2.
Картинки не прилагаются)

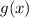 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.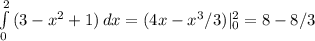
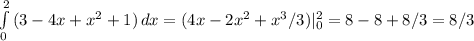
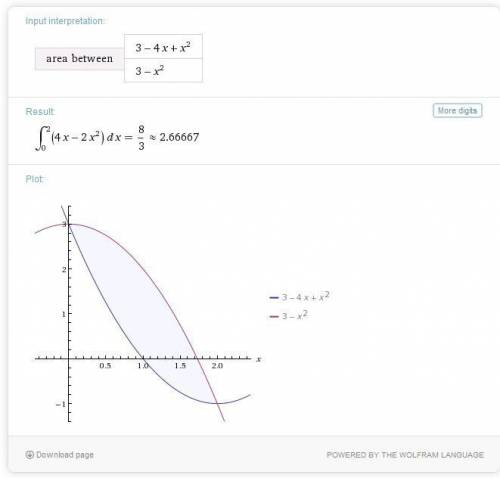
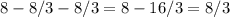 (кв. ед.)
(кв. ед.)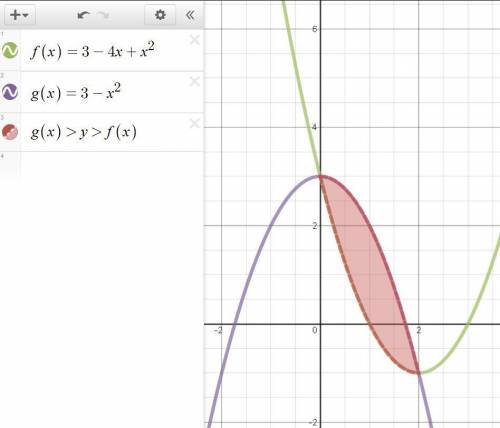
Пусть x и y - стороны прямоугольника.
Р=2(x+y) - его периметр
S=x·y -его площадь
2(x+y)=62
xy=210
x=31-y
y(31-y)=210
x=31-y
31y-y²=210
Решим второе уравнение системы
y²-31y+210=0
Д=121
y₁=(31+11)/2=21
y₂=(31-11)/2=10
y₁=21
x₁=10
y₂=10
x₂=21
ответ: 10 м и 21 м - стороны прямоугольника