ответ:
задать вопрос
войти
октября 16: 24
докажите, что данное уравнение имеет целые корни и найдите их: х^(2)=(√(7−2×√(6))−√(7+2×√()
ответ или решение1
андреева анна
раскроем скобки и решим уравнение, при этом воспользуемся формулами сокращенного умножения:
(a - b)2 = a2 - 2 *a * b + b2.
(a - b)* (а + b) = a2 - b2.
(√(7 - 2 * √6) - √(7 + 2 * √6)) 2 = (√(7 - 2 * √6))2 - 2 * √(7 - 2 * √6) * √(7 + 2 * √6) + √(7 + 2 * √6))2 = 7 - 2 * √6 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) + 7 + 2 * √6 = 14 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) = 14 - 2 * √(72 - (2 * √6) 2) = 14 - 2 * √(49 - 4 * 6) = 14 - 2 * √(49 - 24) = 14 - 2 * √25 = 14 - 2 * √52 = 14 - 2 * 5 = 14 - 10 = 4.
следовательно:
х2 = 4.
х = √4.
х1 = 2; х2 = -2.
ответ: уравнение х2 = (√(7 - 2 * √6) - √(7 + 2 * √6)) 2 имеет корни х1 = 2; х2 = -2
объяснение:
ответ:
задать вопрос
войти
октября 16: 24
докажите, что данное уравнение имеет целые корни и найдите их: х^(2)=(√(7−2×√(6))−√(7+2×√()
ответ или решение1
андреева анна
раскроем скобки и решим уравнение, при этом воспользуемся формулами сокращенного умножения:
(a - b)2 = a2 - 2 *a * b + b2.
(a - b)* (а + b) = a2 - b2.
(√(7 - 2 * √6) - √(7 + 2 * √6)) 2 = (√(7 - 2 * √6))2 - 2 * √(7 - 2 * √6) * √(7 + 2 * √6) + √(7 + 2 * √6))2 = 7 - 2 * √6 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) + 7 + 2 * √6 = 14 - 2 * √((7 - 2 * √6) * (7 + 2 * √6)) = 14 - 2 * √(72 - (2 * √6) 2) = 14 - 2 * √(49 - 4 * 6) = 14 - 2 * √(49 - 24) = 14 - 2 * √25 = 14 - 2 * √52 = 14 - 2 * 5 = 14 - 10 = 4.
следовательно:
х2 = 4.
х = √4.
х1 = 2; х2 = -2.
ответ: уравнение х2 = (√(7 - 2 * √6) - √(7 + 2 * √6)) 2 имеет корни х1 = 2; х2 = -2
объяснение:
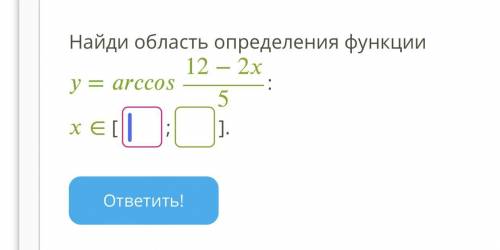
-1 ≤ (12 - 2x)/5 ≤ 1
-5 ≤ 12 - 2x ≤ 5
-5 - 12 ≤ -2x ≤ 5 - 12
-17 ≤ -2x ≤ -7
17 ≥ 2x ≥ 7
7 ≤ 2x ≤ 17
7/2 ≤ x ≤ 17/2
3,5 ≤ x ≤ 8,5
x ∈ [3,5; 8,5]