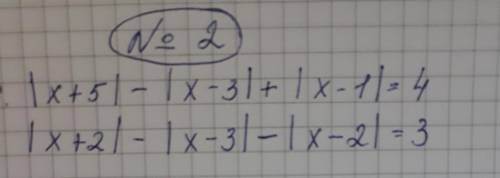
F'(x) = f(x)
((x-1)²)' = 2(x-1)
Первообразная F(x) = (x-1)²+c - общий вид
у=2(х-1) = 2х-2 - график прямая
1. чертим систему координат; отмечаем начало координат - точку О (0; 0), отмечаем стрелками положительное направление: вправо и вверх; подписываем оси : вправо - х, вверх - у; отмечаем единичные отрезки по каждой оси в 1 клетку.
2) для построения прямой достаточно двух точек, занесем их координату в таблицу:
х= 0 2
у= -2 2
3) отметим точки (0; -2) и (2; 2) на координатной плоскости; проведем через данные точки прямую линию; подпишем график функции у= 2х-2
Всё!
а)(-1; 4,5)
б) (-∞;-7)∪(7;+∞)
в) любые х
Объяснение:
Для того чтобы решить квадратное неравенство мы первом делом приравниваем его к нулю и решаем как квадратное уравнение, то есть:
а)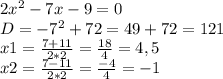
Далее отмечаем эти две точки на координатной прямой и определяем знак на одном из её участков. Я возьму средний участок, а конкретнее число 0 (оно же из среднего участка). Подставлю в уравнение: 2*0-7*0-9, число получу отрицательное, значит на этом промежутке ставлю знак "-". При переходе через корень уравнения( в нашем случае -1 и 4,5) нак меняется на противоположный, то есть на концах воординатной прямой мы получим два плюса.
Смотрим на знак неравенсва: нам нужен участок меньший 0, то есть отрицательный, значит ответ (-1; 4,5). Скобки круглые так как неравенство строгое.
Аналогично далее:
б)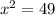
х1= -7
х2=+7
Отметим на числовой прямой и определим знак, я сново подствлю 0 (из центрального интервала) и получая отрицательное число, значит положительные знаки(а они нам и нужны) мы получим на концах данной числовой прямой: (-∞;-7)∪(7;+∞)
в)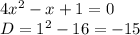
Значит пересечения с осью нет, ветви положительные и парабола находится над числовой прямой. Так как у нас в неравенстве знак "больше", то вопрос заключается в том, при каком х парабола находится выше прямой ох. В нашем случае при любом х.