ответ:√(x - 2) является x > = 2.
Объяснение:
Опишем функцию для нахождения области определения
Функция является сложной, так как выражение под корнем имеет выражение х - 2;
Функция имеет квадратный корень;
Из квадратного корня, не возможно извлечь отрицательное число;
Область определения функции - это те значения х, которое можно подставить в функцию. Отсюда делаем вывод, что областью определения функции является выражение под корнем больше или равно 0.
Находим область определения функции
Выражение под корнем равно х - 2. Так как, оно должно быть больше или равно 0, то отсюда получаем:
x - 2 > = 0;
Известные значения переносим на одну сторону, а неизвестные на другую сторону. При переносе значений, их знаки меняются на противоположный знак. То есть получаем:
x > = 0 + 2;
x > = 2;
Значит, областью определения функции y = √(x - 2) является промежуток x > = 2;
Проверка
Подставим значение х = 6, которое удовлетворяет условию x > = 2 в функцию y = √(x - 2), тогда получим:
y = √(6 - 2);
y = √4;
y = 2;
Значит, при х > = 2 из квадратного корня извлекаются положительные числа. Если же, если было бы < 2, то квадратный корень из отрицательного числа не извлекается.
а)2
б)1
в)3
г) если 5 это ∅ то правильный ответ 5
Объяснение:
а)Переносишь 4 на другую сторону уравнения
х2>-4
А так как степенная функция с парным показателем всегда либо положительная либо 0
То х любое число
б)Так же переносишь 4
Дальше получается х2>4
Тогда |x|>2
x>2,x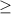 0
0
-x>2,x<0
Находим пересечение:
x∈(2,+∞)
x∈(-∞,-2)
в)Как обычно переносим 4
Получается:x2<4
|x|<2
Рассматриваешь все случаи:
x<2,x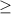 0
0
-x<2,x<0
Находишь пересечение:
x∈[0,2)
x∈(-2,0)
Объединяешь:x∈(-2,2)
г)Переносишь 4:
х2<-4
А это невозможно по этому ∅
A-лежат
Б-не лежат
С-не лежат
Д-не лежат
Е-лежат
Ф-не лежат