1 шоколадка - 25 руб.
Акция: 2+1
Сумма - 130 руб.
25*2=50 руб.- 2 шоколадки
По акции: 50 руб. - 3 шоколадки
130/50=2(ост.30) - 2 целых набора из 3-х шоколадок и 30 руб. останется
50*2=100 руб.; 3*2=6 - шоколадок можно купить на 100 руб.
30/25=1 (ост.5) - на 30 руб. можно купить 1 шоколадку за полную цену, и 5 руб. - сдача
6+1=7 шоколадок можно купить в воскресенье
Проверка: 50/3=16 2/3 руб. - шоколадка по акции
16 2/3 * 6 =50/3 * 6 = 300/3=100 руб. - 6 шоколадок по акции
130-100=30 руб. останется
30-25=5 руб. сдачи
7 шоколадок можно купить на 130 руб. в воскресенье - 6 по акции и 1 - полная цена
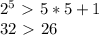 .
. 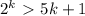 .
.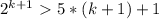
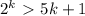 =>
=> 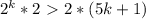 =>
=> 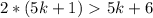
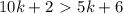 .
. 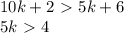
 .
.
(b-4)(b+4)(b²+16)-(b²-5)²=(b²-16)(b²+16)-(b⁴-10b²+25)=b⁴-256-b⁴+10b²-25=10b²-281
b=1
10*1²-281=-271
Объяснение: