Решить уравнение а) 2 sin х - 3 cos^2 x + 2 = 0; б) 5 sin^2x - 3 sin x cos х - 2 cos^2x = 0. - id211848820200221 от 12СоловьёваАнна 21.02.2020 02:32

Question

Алгебра: Решить уравнение а) 2 sin х - 3 cos^2 x + 2 = 0; б) 5 sin^2x - 3 sin x cos х - 2 cos^2x = 0.

12СоловьёваАнна · Accepted Answer

В обоих случаях рассматриваем прямоугольный треугольник с одним из углов 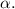$\alpha .$

В первом случае примем прилежащий к углу 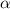$\alpha$ катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 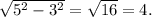$\sqrt{5^2-3^2}=\sqrt{16}=4.$ Синус угла 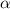$\alpha$ есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.

Во втором случае примем катет, лежащий против 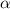$\alpha$ за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 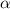$\alpha$ есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.

Решить уравнение а) 2 sin х - 3 cos^2 x + 2 = 0; б) 5 sin^2x - 3 sin x cos х - 2 cos^2x = 0.

MOGZ ответил