1. Найдите производные функций
А) y= x6 y`=6x5
б) y = 2 y`=0
в) y=5/x y`=-5/x^2
г) y = 3-5x y=-5
д) y= 8 √x + 0,5 cos x y`=4/Vx -0.5sinx
е) y=sinx / x y`={xcosx-sinx}/x^2
ж) y= x ctg x y`={ctgx-x/sin^2x}=cosx/sinx- x/sin^2x={cosxsinx-x}/sin^2x
з) y= (5x + 1)^7 y`=5*7(5x+1)^6=35(5x+1)^6
2.Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции:
y= x^8/8 – x^5/5 - x √3 – 3 в точке x0= 1
y`=x^7-x^4-V3 tga=y`(1)=1-1-V3=-V3 a=120*
3. Вычислите если f(x)=2cos x+ x2- +5 что надо?
4. Прямолинейное движение точки описывается законом s=t4 – t2(м). Найдите ее скорость в момент времени t=3с.
v=s`=4t3-2t
v(3)=4*27-2*3=108-6=102 м/с
5. Найдите все значения х, при которых выполняется неравенство f/(x)<0, если
f(x)= 81x – 3x3
f`=81-9x^2=9(3-x)(3+x)
-3 3
- + -
xe(-oo,-3)U(3,+oo)
6. Найдите все значения х, при которых выполняется равенство f/(x)=0, если f(x)=cos2x - x√3 и x€[0,4π].
Сначала решаем соотв. однородное уравнение, запишем его характеристическое уравнение
\lambda^2-6\lambda+9=0λ
2
−6λ+9=0
имеем случай кратных действительных корней, значит общее решение однородного уравнения
y(x)=C_1*e^{3x}+C_2*x*e^{3x}y(x)=C
1
∗e
3x
+C
2
∗x∗e
3x
Далее применим метод вариации. Тогда
\begin{gathered} \left( < br / > \begin{array}{cc} < br / > e^{3 x} & e^{3 x} x \\ < br / > 3 e^{3 x} & 3 x e^{3 x}+e^{3 x} \\ < br / > \end{array} < br / > \right) * \left( < br / > \begin{array}{c} < br / > C_1'(x) \\ < br / > C_2'(x) \\ < br / > \end{array} < br / > \right)=\left( < br / > \begin{array}{c} < br / > 0 \\ < br / > 9 x^2-12 x+2 \\ < br / > \end{array} < br / > \right) \end{gathered}
⎝
⎛
<br/>
<br/>e
3x
<br/>3e
3x
<br/>
e
3x
x
3xe
3x
+e
3x
<br/>
⎠
⎞
∗
⎝
⎛
<br/>
<br/>C
1
′
(x)
<br/>C
2
′
(x)
<br/>
<br/>
⎠
⎞
=
⎝
⎛
<br/>
<br/>0
<br/>9x
2
−12x+2
<br/>
<br/>
⎠
⎞
Откуда получим
C_1'(x)=-e^{-3x}*x*(9x^2-12x+2), < br / > C_2'(x)=e^{-3x}*(9x^2-12x+2)C
1
′
(x)=−e
−3x
∗x∗(9x
2
−12x+2),<br/>C
2
′
(x)=e
−3x
∗(9x
2
−12x+2)
Интегрированием находим
C_1(x)=-e^{-3 x}(x^2 - 3 x^3)+A, C_2(x)=e^{-3 x} (2 x - 3 x^2)+BC
1
(x)=−e
−3x
(x
2
−3x
3
)+A,C
2
(x)=e
−3x
(2x−3x
2
)+B
Следовательно общее решение уравнения запишется как (переобозначим константы A и B )
y(x)=(-e^{-3 x}(x^2 - 3 x^3)+C_1)*e^{3x}+(e^{-3 x} (2 x - 3 x^2)+C_2)*x*e^{3x}y(x)=(−e
−3x
(x
2
−3x
3
)+C
1
)∗e
3x
+(e
−3x
(2x−3x
2
)+C
2
)∗x∗e
3x
или
y(x)=C_1*e^{3x}+x*C_2*e^{3x}+x^2y(x)=C
1
∗e
3x
+x∗C
2
∗e
3x
+x
2
Соотв. постоянные для нашей задачи Коши находятся из системы
\left \{ {{y(0)=0} \atop {y'(0)=3}} \right.{
y
′
(0)=3
y(0)=0
Откуда
\left \{ {{C_1=0} \atop {C_2=3}} \right.{
C
2
=3
C
1
=0
Получаем функцию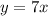
Нетрудно заметить, что при
, значение функции равно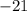 
, а значит график линейной функции 
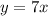проходит через точку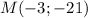 
Задача решена.