

7)
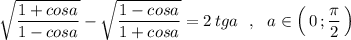
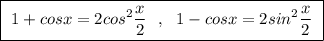
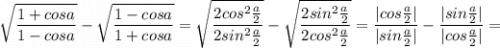
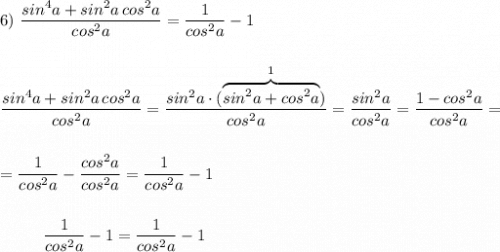
Так как по условию задан угол, лежащий в 1 четверти, то тригонометрические функции будут принимать положительные значения. А значит модули триг-их ф-ций будут равны функциям, записанным под знаком модуля.
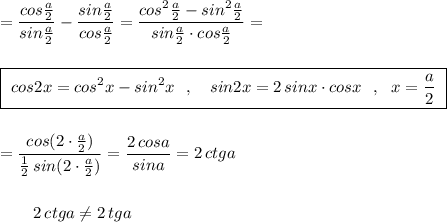
Заданное тождество не является тождеством .
![\displaystyle \sqrt[3]{2}= 2^{ \frac{1}{3} } \\ \displaystyle \sqrt[5]{3}= 3^{ \frac{1}{5} }](/tpl/images/0869/4658/e78b1.png)
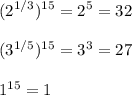
![\displaystyle \sqrt[3]{2} \ \textgreater \ \sqrt[5]{3}\ \textgreater \ 1](/tpl/images/0869/4658/44fe6.png)
ответ: во вложении
Объяснение: там же.
в этом у меня ошибка или у вас опечатка? двумя и не 2 tgα, а 2 ctgα получилось.)
√((1-cosα)/(1+cosα))-√((1+cosα)/(1-cosα))