В решении.
Объяснение:
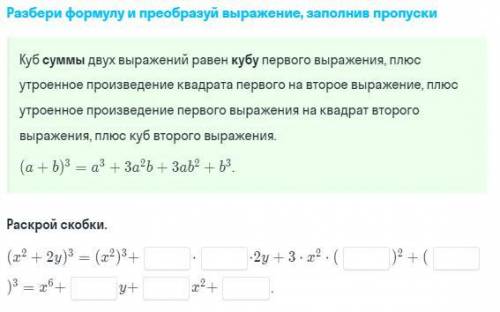
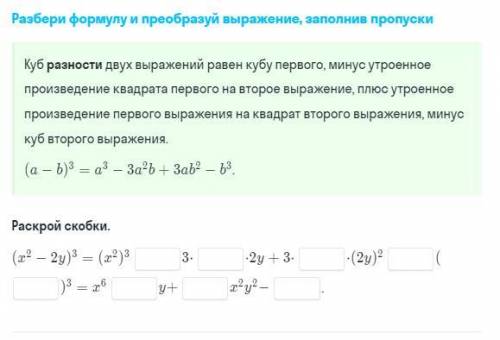
Разберите формулу и преобразуйте выражение, заполнив пропуски:
1) (х² + 2у)³ = (х²)³ + 3*(х²)²*2у + 3*х²*(2у)² + (2у)³ =
= х⁶ + 6х⁴у + 12х²у² + 8у³;
2) (х² - 2у)³ = (х²)³ - 3*(х²)²*2у + 3*х²*(2у)² - (2у)³ =
= х⁶ - 6х⁴у + 12х²у² - 8у³.
ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х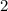
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
ответ:
1)
пусть х км/ч - скорость пассажирского поезда, тогда скорость товарного поезда составляет х-20 км/ч.
пассажирский поезд пройдет расстояние, равное 120 км, за t=s: v= часов. товарный поезд пройдет это же расстояние за
часов, что на 1 час больше.
составим и решим уравнение:
- = 1 (умножим на х(х-20), чтобы избавиться от дробей)
- =1*x(x-20)
120*х - 120*(х-20)=х²-20х
120х-120х+2400-х²+20х=0
х²-20х-2400=0
d=b²-4ac=(-20)²+4*1*(-2400) = 400+9600=10000 (√10000=100)
x₁ = = 60
x₂ = = -40 - не подходит, поскольку х < 0
скорость пассажирского поезда равна 60 км/ч, тогда скорость товарного составит х-20=60-20=40 км/ч.
проверка:
120: 60=2 (часа) - пассажирский поезд проедет расстояние, равное 120 км.
120: 40=3 (часа) - товарный поезд проедет расстояние, равное 120 км.
3-2=1 час
2
1) пусть х км/ч — скорость второго автомобиля ( х > 0).
2) тогда (х + 10) км/ч — скорость первого.
3) (300 : (х + 10)) ч. — столько времени уходит у первого автомобиля на преодоление пути в 300 км.
4) (300 : х) ч. — за столько времени второй автомобиль проезжает те же 300 км.
5) по условию первый автомобиль тратит на данный путь на 1 час меньше, чем второй, поэтому записываем равенство:
300 : х - 300 : (х + 10) = 1.
6) решаем уравнение:
300 * (х + 10) - 300 * х = х * (х + 10);
300х + 3000 - 300х = х^2 + 10х;
х^2 + 10х - 3000 = 0.
по теореме виета находим, что х1 = -60, х2 = 50
7) так как -60 < 0, то х1 не является решением .
8) значит, х = 50 км/ч — скорость второго автомобиля.
9) узнаем скорость первого:
50 + 10 = 60 км/ч.
ответ: 60 и 50 км/ч.
Объяснение:
1. +3 × (2y)² надеюсь чемто