Задание 1.
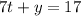
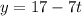
ответ: 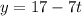
или 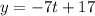
Задание 2. Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 390 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 685 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?
Решение.
Пусть х руб. - стоит один детский билет.
По условию 2 детских билета и один взрослый стоят 390 рублей, значит,
(390-2х) руб. - стоит один взрослый билет.
Ещё в условии сказано, что 3 детских билета и 2 взрослых стоят всего 685 рублей.
Получаем уравнение:
3х + 2 · (390-2х) = 685
3х + 780 - 4х = 685
-х = - 95
х = - 95 : (-1)
х = 95 руб. - стоит один детский билет.
390-2·95=200 руб. - стоит один взрослый билет.
Детский билет стоит 95 рублей,
а взрослый билет стоит 200 рублей.
1. Доведем подкоренные выражения до куба суммы и разности
(a - b)³ = a³ - 3a²b + 3ab² - b³
(a + b)³ = a³ + 3a²b + 3ab² + b³
(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/2³
(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 2³
∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1
ответ ОДИН
2. сделаем по другому
a = 2 + √5
b = 2 - √5
∛(2 + √5) + ∛(2 -√5) = c
∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)
a + b = 2 + √5 + 2 - √5 = 4 (формула 2)
∛a + ∛b = c
∛a = c - ∛b (возводим в куб) (формула 3)
a = c³ - 3c²∛b + 3c∛b² - b
c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c
c³ + 3c - 4 = 0
c³ + c² + 4c - c² - c - 4 = 0
c²(c - 1) + c(c -1) + 4(c-1) = 0
(c - 1)(c² + c + 4) = 0
вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c
первая скобка c = 1
вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)
ответ 1