
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
А6 - 1,3
В1 - (20;20)
В2 - (2;0)
С1 - 2
С2 - (фотка)
Объяснение:
А6. решение на фото
В1. чтобы найти координату пересечения графиков функции нужно их прировнять
Найдём Y если подставим полученное значение Х в функцию (можно подставить в любую)
Точка пересечения графиков функции имеет следующие координаты (20;20)
В.2
Ось абсцисс - это ось ОХ
Чтобы найти координату пересечение графика функции с осью абсцисс
Нужно прировнять Y к 0, так как нам нужно пересечение графика функции с осью абсцисс
Точка пересечение графика функции с осью абсцисс имеет следующие координаты (2;0)
С.1
Мы имеем функцию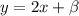 и точку с координатами (0;2)
и точку с координатами (0;2)
Чтобы найти b мы подставим координаты точки в функцию
С.2 решение на фото
(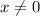 так как при делении любого выражения на 0 получается неопределённое выражение)
так как при делении любого выражения на 0 получается неопределённое выражение)