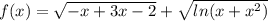
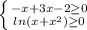
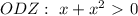я не понимаю алгебра 7 класс учитель глуп (2d-m)(2d+m)
(2n-s)2
(3w+c)2
(2a-3b)(2a+3b)

👇

Увидеть ответ

Ответ:

dimadementev2

21.11.2020

1) (2d-m)(2d+m)= 4d²+2dm-2dm(эти два числа сокращаем)-m²= 4d²-m²

Объяснение:

остальные также)

4,7(89 оценок)

Открыть все ответы

Ответ:

TDashaS

21.11.2020

Здравствуйте. Для решения данного задания следует заметить, что формула практически напоминает полный квадрат выражения. Однако это бы случилось если бы последнее число 25 было бы со знаком +. Поэтому представим -25 как 25-50. Получим 9x^2 + 30x + 25 - 50. Cвернем три первых в полный квадрат (3x + 5)^2 - 50. Полный квадрат всегда является неотрицательным числом, а его минимальное значение 0 при x = -5/3. Соотвественно так как этот x наименьшая переменная то для нее посчитаем и наименьшее выражение. Оно будет равно -50.

4,7(46 оценок)

Ответ:

manechka2007

21.11.2020

$f(x)=\sqrt{-x+3x-2}+\sqrt{ln(x+x^2)}$
Область определения - это множество всех допустимых значений аргумента функции (иксов). Так как квадратный корень существует только для неотрицательных действительных чисел, получаем, что подкоренные функции будут больше либо равняться нулю, запишем это в систему, так как это должно быть одновременно:
$\left \{ {{-x+3x-2\geq0} \atop {ln(x+x^2)\geq0}} \right. 
$
Теперь решаем полученную систему:
Сначала находим ОДЗ:
область определения логарифма от x это только положительные числа, то есть функция под логарифмом больше нуля:
$ODZ:\ x+x^2\ \textgreater \ 0$ Находим решения данного неравенства методом интервалов, то-есть сначала находим нули функции: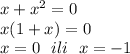
$x+x^2=0
\\x(1+x)=0
\\x=0\ \ ili\ \ x=-1$
y=x^2+x

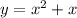это квадратическая функция, график которой -парабола, ветками вверх, которая пересекает ось OX в точках (0;0) и (-1;0), ее вершина располагается в точке, которая рассчитывается следующим образом: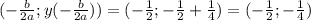 $(-\frac{b}{2a}; y(-\frac{b}{2a}))=(-\frac{1}{2};-\frac{1}{2}+\frac{1}{4})=(-\frac{1}{2};-\frac{1}{4})$
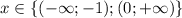Значит при $x\in \{(-\infty;-1);(0;+\infty)\}$ функция будет больше нуля, то-есть ОДЗ: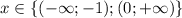 $x\in \{(-\infty;-1);(0;+\infty)\}$
Теперь решаем саму систему:
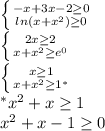
$\left \{ {{-x+3x-2\geq0} \atop {ln(x+x^2)\geq0}} \right.
\\ \left \{ {{2x\geq2} \atop {x+x^2\geq e^0}} \right.
\\ \left \{ {{x\geq1} \atop {x+x^2\geq 1^*}} \right.
\\^*x^2+x\geq 1
\\ x^2+x-1\geq 0$
Решаем данное неравенство также методом интервалов:
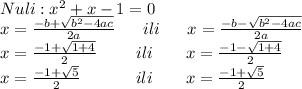
$Nuli: x^2+x-1=0
\\x=\frac{-b+\sqrt{b^2-4ac}}{2a}\ \ \ \ \ ili\ \ \ \ \ x=\frac{-b-\sqrt{b^2-4ac}}{2a}
\\x=\frac{-1+\sqrt{1+4}}{2}\ \ \ \ \ \ \ ili \ \ \ \ \ \ x=\frac{-1-\sqrt{1+4}}{2}
\\x=\frac{-1+\sqrt{5}}{2} \ \ \ \ \ \ \ \ \ \ ili \ \ \ \ \ \ x=\frac{-1+\sqrt5}{2}$
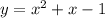y=x^2+x-1

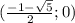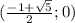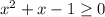- это квадратическая функция, график которой парабола ветками вверх, которая пересекает ось OX в точках $(\frac{-1-\sqrt{5}}{2};0)$ и $(\frac{-1+\sqrt{5}}{2};0)$ Значит $x^2+x-1\geq0$ при $x\in \{ (-\infty ;\frac{-1-\sqrt{5}}{2}];[\frac{-1+\sqrt{5}}{2}; +\infty)\}$
Теперь собираем все корни неравенств и ОДЗ в одну систему:
$\left \{ {{x\geq 1} \atop {x\in \{ (-\infty ;\frac{-1-\sqrt{5}}{2}];[\frac{-1+\sqrt{5}}{2}; +\infty)\}} \atop } \right. 
\\ODZ: x\in \{(-\infty;-1);(0;+\infty)\}
$
Получаем ответ:
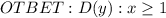
$OTBET: D(y): x\geq 1$
График данной функции на картинке ниже
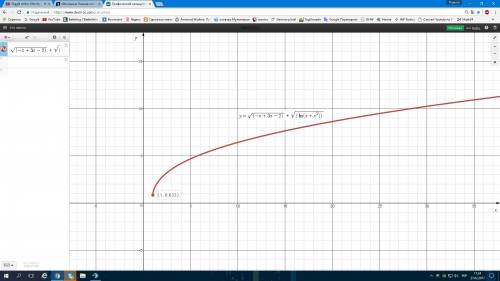
Найдите область определения функции f(x)=sqrt(-x+3x-2)+ sqrt(ln(x+x^2)) !