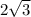
а² – b² = 2017
а² – b² = (а – b) * (а + b)
(а – b) * (а + b) = 2017
Число 2017 простое, поэтому имеет только два натуральных делителя 1 и 2017.
2017 = 1 * 2017
Поэтому
(а – b) * (а + b) = 1 * 2017
Имеем систему
{а + b = 2017
{а – b = 1
Из второго уравнения получим
а = b + 1
Подставим в первое уравнение
(b + 1) + b = 2017
2 b = 2017 - 1
2 b = 2016
b = 2016 : 2
b = 1008
а = 1008 + 1 = 1009
Проверка чисел а = 1009; b = 1008
1009² – 1008² = 2017
1018081 – 1016064 = 2017
2017 = 2017
ответ: существует только 1 вариант натуральных чисел разность квадратов которых равна числу 2017. Это числа 1008 и 1009.
Часть 1
1)Верно
Односторонние углы при параллельных прямых дают сумму углов в 180 °
2)Верно
Смежные углы дают в сумме 180 °
3)Неверно
Эти прямые могут быть параллельные,а они никогда не пересекаются
4)Верно отчасти
Смежные углы могут быть равны,только когда оба угла = 90 °, в остальных случаях они не равны
Часть 2
14)9х - 3(12 - 7x) = 5(6x - 7) - 1
9х-36+21х = 30х-35-1
9х+21х-30х = -35-1+36
0х = 0
13) 1) 8 - 3 = 5(ч) - турист шёл на подъём
Пусть х - скорость на спуске, тогда х+1 - скорость на подъём
5*(х+1)+3х = 21
5х +5+3х = 21
5х+3х =21 -5
8х = 16
х = 16:8
х = 2 (км/ч) - скорость туриста на спуске
16) ответ в приложении
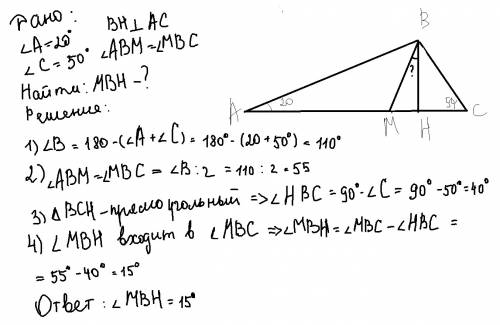
Объяснение:
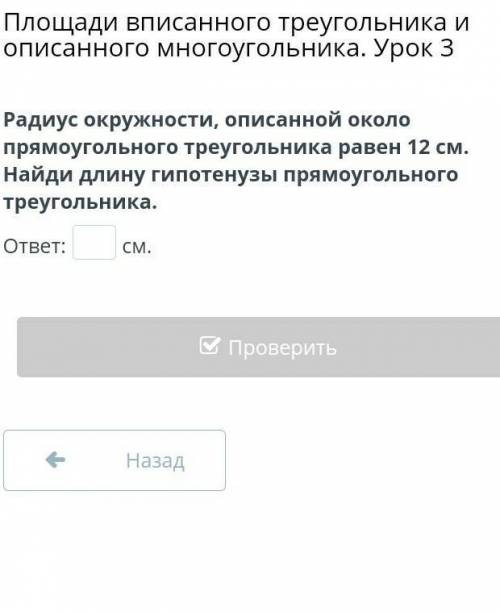
R=12 см
Гипотенуза с=2×R=2×12=24 cм
ответ : 24 см