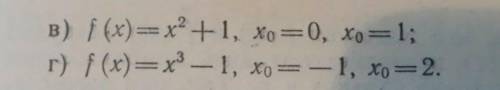
Так, ну смотрите. Они просто обрезали решение. Если решать подробнее, то получается вот так:
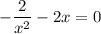
Минус перед первой дробью мы можем поставить в числитель, сути это не поменяет. Приводим слагаемые к общему знаменателю, для этого домножаем второе на 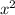 :
:
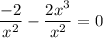
При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитается числитель второй дроби, а знаменатель остаётся прежним.
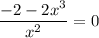
Дробь равна нулю тогда, когда её числитель равен нулю, а знаменатель отличен от нуля, этот нюанс в приложенном решении учтён. Приравниваем числитель к нулю:

Ну и далее уже как на картинке.
а)
т.к график проходит через начало отсчёта, то он график прямой пропорциональности вида: y=kx
Найдём точку, лежащую на графике с координатами (2;1). x=2, y=1
1=k×2
k=1:2
k=0,5
Этот график: y=0,5x
б)
График не проходит через начало отсчёта и он паралеллен оси абсцисс.
Следовательно:
Этот график вида: y=b, где b-некоторое число.
Судя по графику b=2.
Этот график: y=2
в)
График не проходит через начало отсчёта и он не паралеллен одной из осей. Следовательно он вида: y=kx+b
Точки пересечения: (0;3) и (2;0)
Подставим и получим:
3=k×0+b
0=k×2+b
Заметим, что в первом уравнении b=3. т.к k обратится в ноль.
Запишем в новом виде второе уравнение и получим:
0=k×2+3
2k=-3
k=-3:2
k=-1,5
Нашли все неизвестные переменные и уже, наконец, уравнение этого графика: y=-1,5x+3