Объяснение:
Геродот көрген, естіген, оқыған материалдарын жинақтап, артына «Тарих» атты үлкен еңбек қалтырды. Кейіннен александриялық ғалымдар оның еңбегін тоғыз музаға сәйкестендіріп, тоғыз кітапқа бөлген. Геродот алғашқы төрт кітабында Лидия, Мидия мемлекеттері, Ахемен әулеті жөнінде жазып, олардың Мысырға, Вавилонға, сақтарға қарсы жорықтарына тоқталады. Қалған бес кітабы грек-парсы соғысына (біздің заманымыздан бұрынғы 500 – 449) арналған. Онда халықтардың тарихымен қатар этнографиясы, діні, әдебиеті, мемлекеттердің ішкі-сыртқы саясаты, экономикасы берілген. Шығарманың төртінші кітабында парсы патшасы Дарий Гистасптың сақтарға қарсы жорығы баяндалған. Онда сақтар елі жөнінде аса құнды мәліметтер ұшырасады. Қолжазбаларының ішінде бізге жеткен Флоренция нұсқасы ағылшын, орыс, т.б. тілдерге аударылған. Герадот сақтарды азиялық скифтер деп атаған.Геродот б.з.б. 40-жылдардан бастап Грекияның көптеген облыстарында, парсы патшалығында болып, ионий логографтары сияқты жатжерліктердің тарихы мен этнографиясын зерттеді. Кейінірек ол солтүстік Қара теңіз жағалауында, Египетте, Финикияда, Вавилонда және еуропалық Грекияның көптеген қауымдастықтарында болды. Ал оның екінші рухани отаны – Афины болды. Афиныда сол дәуірдің танымал қайраткерлері Периклмен және Софоклмен танысты. Дүниетанымы, өмірлік көзқарастары сәйкес келгендіктен, әсіресе Софоклмен жақсы қарым-қатынаста болды
Грек әлемінде қабылданған қағида бойынша әрбір адам туған жерінде ғана, яғни сол елдің азаматы болғанда ғана саясатпен айналысуға құқылы болатын. Геродот болса Самоста да, Афиныда да жатжерлік болып есептелді. Осы жағдайлар оның өмірлік ұстанымы саясат емес, тарих болуына әсер еткен болуы мүмкін. Б.з.б. 444 жылы оңтүстік Италияда барлық гректерге ортақ Фурия колониясы құрылғанда Геродот сол жақтан жер алып, азамат болу құқығына ие болды. Протогор Абдерский жаңа колония үшін бірқатар заңдар жазса, архитектор Гипподам Мипетский қаланың жоспарын сызды. Геродоттың осыдан кейінгі өмірі туралы мәлімет жоқтың қасы. Фурияда ол өзінің тарихи еңбегін аяқтаған болуы керек
См в объяснение, это полезно
Объяснение:
Ну давай начнем с того, что вообще такое область определения.
Область определения - область значений x (или любой другой независимой переменной), при котором функция имеет смысл, то есть имеет значение y
Функция не имеет значения (и значений тоже), когда, например, присутствует деление на 0, а так же, когда подкоренное выражение отрицательно (но последнее - только в рамках действительных чисел, но сейчас мы рассматриваем задачу в этих рамках, иначе это было-бы указано). Это мы сейчас и будем использовать.
11. Давай сразу посмотрим на знаменатели, остальное сейчас не имеет значения
Сначала предположим, в каком случае знаменатель будет равен 0
Квадратный корень равен нулю, когда подкоренное выражение равно нулю, тогда
Тогда, посмотрим на другое условие - подкоренное выражение не должно быть отрицательным, значит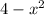
должен быть больше или равен нулю, значит, 
, следовательно, 
=> 
=> 
=> 
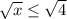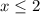и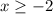 
(это - исключительно совокупность)
Значит, из этого знаменателя мы можем вынести, что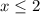
и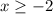 
(если-бы было еще что-то, то данное условие вошло бы с ним в еще одну совокупность)
Посмотрим тогда на знаменатель другой дроби
Здесь все проще - x-1
Тут нет квадратного корня, поэтому - единственное, на что можно обратить внимание - это то, что знаменатель дроби не должен быть равен нулю.
Предположим, что знаменатель равен нулю, тогда x-1=0 => x=1
Так как при этом значении х функция утрачивает смысл, то это значение надо исключить из области определения =>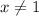
Итак, мы имеем два условия, при соблюдении которых функция будет иметь смысл-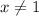
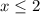и 
и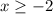 
(последнее- совокупность). При этом, если соблюсти только одно из условий - функция все равно не будет иметь значений. Значит, это тоже будет совокупностью.
Если надо, можно записать в таком виде -![x=\left[\begin{array}{ccc}x\neq 1\\x\leq 2&x\geq -2\end]](/tpl/images/1495/6656/00f1e.png)
(нижнюю строку надо тоже сделать совокупностью, я не могу это сделать на компьютере)
Или так - x ∈ [-2;0)∩(0;2]
В целом, действовать можно по такой схеме - находим знаменатели дробей, смотрим, есть ли в них переменная, если есть - то находим область значений этой переменной, при которых значение знаменателя не будет равно нулю (на промежуточном этапе можно в виде
n). Потом - ищем корни, и находим область определения, при котором подкорное выражение неотрицательное. Потом - объединяем полученные условия в совокупность - и готово