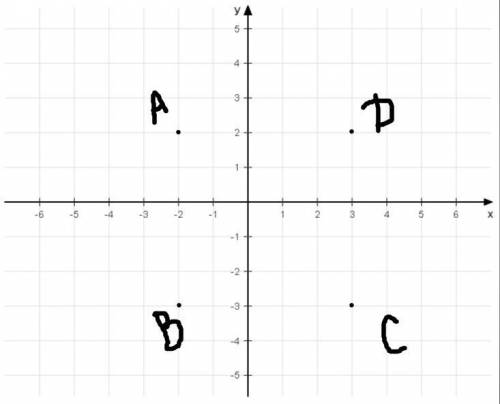
1) координати точки В
В (-2;-3)
2) координати точки перетину діагоналей;
(0,5 ; -0,5)
3) периметр площу прямокутника
Периметр =20
Площадь =25
Объяснение:
A(-2;2); С(3;-3); D(3;2)
Наносим все точки в соответствии с осями координат, получаем:
В (-2;-3)
Мы получаем квадрат, и его диагонали, согласно графику, пересекутся в точке с координатой (0,5 ; -0,5)
Считаем клеточки, соответствующие одной стороне, получаем 5.
Периметр 5*4=20 (периметр это сумма всех сторон, здесь четыре одинаковые стороны)
Площадь 5*5=25 (площадь, это сторона умноженная на другую сторону, или, если это квадрат, то сторона в квадрате)
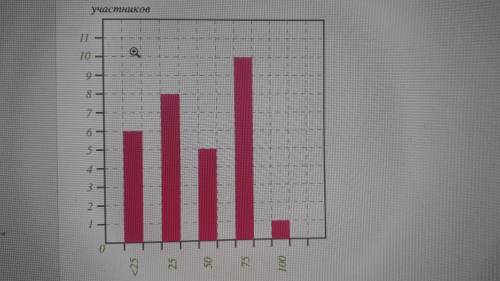
ответ: 16
Объяснение:
Исходя из условий, необходимо учитывать только x>=50
Таким образом по диаграмме проходит 5 участников набравших 10 участников набравших и 1 участник набравший Итого имеем 16 человек.