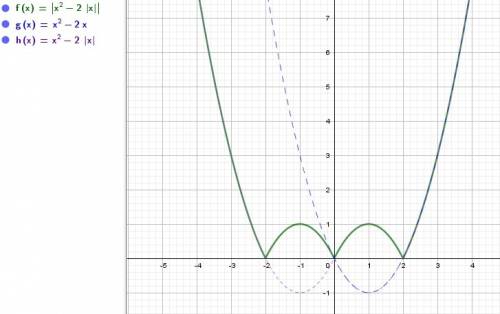
1. Строим сначала график функции y = x² - 2x. Графиком квадратичной функции является парабола, ветви которого направлены вверх.
(1;-1) - координаты вершины параболы.
2.График функции y = x² - 2x симметрично отобразим относительно оси ординат, получим график функции y = x² - 2|x|
3. Нижнюю часть графика функции y = x² - 2|x| симметрично отобразим относительно оси Ох в положительную часть оси ординат, в результате получим график функции y = |x² - 2|x||
Графиком функции y = a-1 является прямая, параллельная оси Ох.
1) При a-1=0 откуда а=1 графики функций имеют три общих точек, следовательно, уравнение имеет три решения.
2) При 0 < a-1 < 1 откуда 1 < a < 2 графики пересекаются в 6 точках, следовательно уравнение имеет 6 решений.
3) При а - 1 = 1 откуда а=2 графики имеют четыре общих точек, следовательно, уравнение имеет ровно 4 решений
4) При a-1 > 1 откуда a>2 графики имеют две общих точек, значит уравнение имеет два решения
Сначала рассмотрю ОДЗ:
-x - 16 > 0,
√(-x) - 4 > 0,
-x > 0.
x < -16
x < -16
x < 0
ОДЗ: x < -16
Правила для логарифмов, используемые в решении:
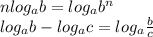
__________________________________
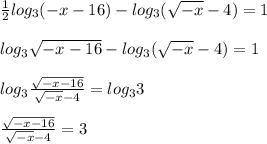
Сделаем замену √(-x) = t, тогда -x= t²:
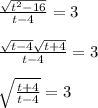
Возведём обе части в квадрат, при таком решении могут возникнуть посторонние корни, их нужно отсеять с ОДЗ (t+4)/(t-4) > 0 или с проверки:
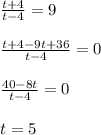
Проведём обратную замену:
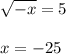
-25 < -16 (проверка, удовлетворяет ли ОДЗ), следовательно найденный корень подходит.
ответ: -25
Y=3cosx-1
1) D(y)=(-∞;+∞)
2) E(y)=?
E(cosx)=[-1;1]
E(3cosx)=[-3;3]
E(3cosx-1)=[-3-1;3-1]
E(3cosx-1)=[-4;2]
3) y=-1 x=?
3cosx-1=-1
3cosx=0
cosx=0
x=π/2+πk, k∈Z
Объяснение:
Область определения - вся числовая ось.