Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)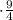 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 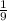 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 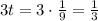 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 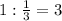 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

Найдём координаты вектора 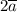 . Для этого все координаты вектора
. Для этого все координаты вектора 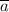 нужно умножить на 2:
нужно умножить на 2:
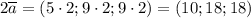
По такому же принципу найдём координаты вектора 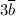 :
:
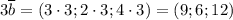
Чтобы найти координаты вектора  , вычтем соответствующие координаты:
, вычтем соответствующие координаты:
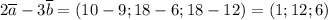
Длина произвольного вектора 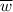 вычисляется по формуле
вычисляется по формуле 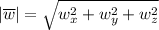 :
:
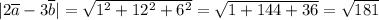
ответ: 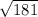 .
.
***
Координаты середины отрезка есть среднее арифметическое координат конца отрезка:
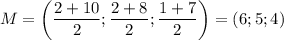
***
По условию точка 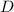 делит сторону
делит сторону 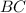 пополам (и так же с двумя другими точками). Найдём координаты точки
пополам (и так же с двумя другими точками). Найдём координаты точки
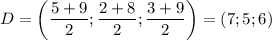
Расстояние между точками 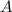 и
и 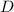 (т. е. длина медианы) равно:
(т. е. длина медианы) равно:

То есть  .
.
То же самое проделаем с двумя другими медианами:
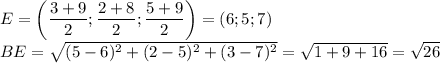
- - - - - - -
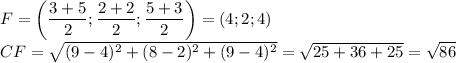
***
Если что-либо будет непонятно — спрашивайте.
(2-2)3-24(z-6)=132-7
Объяснение:
2*3-2*3-24*z+24*6=132-7
6-6-24z+144=125
0-24z=125-144
-24z= -19
19=24z
24z=19
x=19/24