Объяснение:
24.121
я, конечно прощения, но члены арифметической прогрессии обозначаются как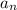 
(у вас это 
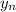) а разность арифметической прогрессии обозначается как b (у вас это d) я буду обзначать так, как принято в математике
1)
а₁₀ = -19
d= -2
применим формулу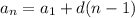 
a₁₀ = a₁ + (-2)*9 = -19 a₁ = -19 +18 = -1
2)
применим ту же формулу
a₅ = a₁ +4d = 13 ⇒ a₁ = 13-4d
a₁₆ = a₁ + 15d = 46 подставим сюда a₁ = 13-4d получим
13-4d +15d = 46 ⇒ 11d = 33 ⇒ d = 3
тогда
a₁ = 13-4d = 13 - 12 = 1
24.123
всё та же формула
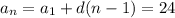
8 +3(n-1) = 24
8+3n -3 = 24
3n = 24-5 = 17 здесь нет целого решения для n ⇒ 24 не есть член арифметической прогрессии
В решении.
Объяснение:
1. Найдите значение выражения: 3,5 ∙ 2³ -3⁴ = 3,5*8 - 81 = 28-81 = -53.
2. Представьте в виде степени выражение:
1) x⁶ ∙ x⁸ = х⁶⁺⁸ = х¹⁴.
2) x⁸ : x⁶ = х⁸⁻⁶ = х².
3) (x⁶)⁸ = х⁶*⁸ = х⁴⁸.
4) (x⁴)³ ∙ x² : x⁹ = (х⁴*³) * х² : х⁹ = х¹² * х² : х⁹ = х¹²⁺²⁻⁹ = х⁵.
3. Преобразуйте выражение в одночлен стандартного вида:
Одночлен называется представленным в стандартном виде , если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных.
Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена, сумму показателей степени переменных называют степенью одночлена.
1) – 6a⁴ b⁵ ∙ 5b² ∙ a⁶ = (-6*5)a⁴⁺⁶b⁵⁺² = -30a¹⁰b⁷.
2) (- 6m³ n²)³ = (-6)³m³*³n²*³ = -216m⁹n⁶.
1. Представьте в виде многочлена стандартного вида выражение:
Привести многочлен к стандартному виду, значит, привести подобные члены и расположить одночлены в порядке убывания степеней и в алфавитном порядке.
Степенью многочлена называется наибольшая из степеней его слагаемых.
1) (6x² – 5x + 9) –(3x² + x – 7) =
= 6x² – 5x + 9 - 3х² - х + 7 =
= 3х² - 6х +16.
2) Вычислите:
(5¹³ * 125²)/25⁹ =
= [5¹³ * (5³)²]/(5²)⁹ =
= (5¹³ * 5⁶)/5¹⁸ =
= 5¹⁹/5¹⁸ = 5.
3) Упростите выражение:
128x² y³ * (-1/4 xy⁵)³ =
= 128x² y³ * (-1/4)³х³у¹⁵ =
= 128x² y³ * (-1/64)х³у¹⁵ =
= -(128/64)х²⁺³у³⁺¹⁵ =
= -2х⁵у¹⁸.
Объяснение:
Это график функции y=sin(2x), симметричный относительно оси ОУ.