1 Последовательность (аn) задана рекуррентно: а1 = 12, an+1 = an – 4 . а) Выпишите первые шесть членов этой последовательности.
б) Есть ли в этой последовательности отрицательные числа? Если да, то
укажите номер какого-нибудь из них.
2 Дана последовательность 0; 3; 8; 15; 24… (cn).
а) Определите правило, по которому строиться последовательность.
б) Запишите следующие два члена в этой последовательности.
в) Задайте эту последовательность формулой ее n-го члена.
Дана арифметическая прогрессия -25, -22, -19… (an).
а) Определите ее разность.
б) Запишите формулу n-го члена этой прогрессии.
в) Выясните, содержится ли в этой прогрессии число 20 и если да, то под каким
номером.
г) Определите, сколько в этой прогрессии отрицательных членов.
д) Найдите a101.
МОЖНО СЕГОЛНЯ?
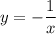и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
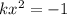и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
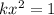и при k<0 это уравнение решений не имеет.
, имеем
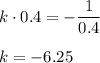
(а·а+1) / а ≥ 2 обе части умножаешь на знаменатель а
а²+1≥ 2·а
а²-2а +1≥0 Сначала приравняй к нулю, найди корни через дискриминант
а²-2а +1=0 Д= b²-4ac= (-2)²-4·1·1= 0 значит корень один!
а = (-b)/ 2a= 2/2 =1
Рисуй луч, лтложи на нём точку а= 1 ( корень)
1⇒
В первом интервале (от -∞ до 1) возьми пробную точку, например 0,
подставь в нерав-во а+ 1/а ≥2 0 +1/0 ≥2 неверно,на ноль делить нельзя
далее возьми проб точку из интервала от 1 до +∞,например 2
подставь в нерав-во 2+1/2≥2 верно, значит ответ буде, учитывая, что на ноль делить нельзя Х∈ от 1 до +∞, включая 1, так как неравенство нестрогое ≥