 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 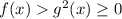 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 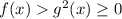 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
Раскрываем модуль
1)
lxl+3x=12
x ≥ 0
x + 3x = 12
4x = 12
x₁ = 3 да
x < 0
-x + 3x = 12
2x = 12
x = 6 нет
2)
lxl-4x=9
x ≥ 0
x - 4x = 9
-3x = 9
x = -3 нет
x < 0
-x - 4x = 9
-5x = 9
x₁ = -9/5 да
3)
2(x-5)-6lxl=-16
x ≥ 0
2(x-5)-6x=-16
2x - 10 - 6x = -16
-4x = -6
x₁ = 3/2 да
x < 0
2(x-5)+6x=-16
2x - 10 + 6x = -16
8x = -6
x₂ = -3/4 да