Как решаются такие уравнения.
Правило звучит таким образом.
В первую очередь нужно перенести в одну сторону от знака равенства все слагаемые, содержащие переменную, а все числовые слагаемые перенести в другую сторону от знака равенства.
Например, во втором 2) примере:
переносим 2х влево, а 4 вправо. При переносе через знак равно меняется знак слагаемого на противоположный.
То есть получаем:
9х + 2х = 48 - 4.
Вычисляем правую и левую части:
11х=44.
После этого находим х, делим правую и левую части уравнения на множитель при х, то есть на 11.
11х / 11 = 44 / 11
х = 4. Это ответ.
в 5) делаем аналогично:
переносим слагаемые с х в одну сторону, числа в другую:
в данном случае перенесем 1.3х вправо, чтобы знак у слагаемого с х был плюс:
6.8 + 2.7 = 0.6х + 1.3х
9.5 = 1.9х
Чтобы дальше решалось проще, умножим правую и левую части на 10 (удобно так избавляться от дробей)
9.5*10=1.9х*10
95 = 19х
Теперь делим правую и левую части на 19:
95/ 19 = 19х / 9
5 = х
х = 5
Развернуть уравнение можно в любой момент в процессе решения.
ответ: х = 5.
6) решается аналогично:
переносим слагаемые с переменным влево, числовые слагаемые вправо:
4/9 * х - 1/6 * х = 9 - 14 = -5, сразу вычисляем правую часть
Для упрощения вычисления умножим правую и левую часть уравнения на 18 - наименьшее число такое, умножение на которое позволит избавиться от дробей в левой части:
4/9 * х * 18 - 1/6 * х * 18 = -5 * 18
4*18/9 * х - 1*18/6 * х = -80
18 делим на 9, получаем 2; 18 делим на 6, получаем 3.
4*2*х - 1*3*х = -80
8х - 3х = -80
5х = -80
Делим правую и левую части на 5:
5х/5 = -80/5
х = -18
ответ: х = -18
Дана функция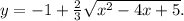
Начнём с выражения под корнем.
Минимум по производной равен: 2х - 4 = 0, х = 2.
Под корнем 4 - 4*2 + 5 = 1.
Минимум всей функции равен -1 +(2/3)*1 = -1/3.
Перенесём -1 влево и возведём обе части уравнения в квадрат.
(у + 1)² = (4/9)(x² - 4x + 5).
В правой части выделим полный квадрат.
x² - 4x + 5 = (x² - 4x + 4) - 4 + 5 = (x - 2)² + 1.
Правая часть примет вид (4/9)((x - 2)² + 1) = (4/9)(x - 2)² + (4/9).
Перенесём квадрат с х влево:
(у + 1)² - (4/9)(x - 2)² = 4/9.
Разделим обе части на 4/9.
((у + 1)²)/(4/9) - ((x - 2)²/1) = 1.
Получили уравнение гиперболы, повёрнутой на 90 градусов.
Но в соответствии с заданием, только верхняя часть этой гиперболы удовлетворяет заданному уравнению.