Пусть х - производительность первого рабочего, а у - производительность второго рабочего. Тогда за 4 дня они могут выполнить совместно 4(х+у)=2/3. Количество дней за которое может выполнить работу первый рабочий 1/х, а второй 1/у. Составим и решим систему уравнений:
4(х+у)=2/3
1/х-1/у=5
х+у=1/6
(у-х)=5ху
у=1/6-х
1/6-х-х=5(1/6-х)*х
1/6-2х=5/6х-5х²
5х²-17/6х+1/6=0 |*6
30х²-17х+1=0
D=17²-4*30=169=13²
x₁=(17+13)/60=1/2 y₁=1/6-1/2<0 не подходит
x₂=(17-13)/60=1/15 у₁=1/6-1/15=3/30=1/10
Значит производительность первого работника 1/15, а второго 1/10.
1:1/15=15 дней выполнит работу первый рабочий
1:1/10=10 дней выполнит работу второй рабочий
ответ за 10 дней и за 15 дней
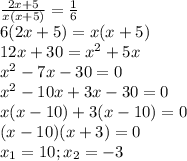
Решение:1) Периметр трапеции равен АВ+ВС+СД+АД, тогда АВ+ВД=64-24-30=10АВ=ВД=5 см., т.к. трапеция равнобедренная.2) Проведем высоты ВН и СМ, тогда четырехугольник ВНМС будет параллелограммом, т.к. ВН || СМ (высоты), ВС || НМ (как основания)ВС=НМ, ВН=СМ по св-ву параллелограмма.3) НМ=24, тогда АН+МД=30-24=6, а АН=МД, т.к. прямоугольные треугольники равны (док-во из первой задачи)АН=МД=3 см.По теореме пифагора найдем ВН=44) Площадь трапеции равна половине произведения оснований, помноженное на высоту, т.е. 24+30/2 * 4=108 см.квадратных