См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
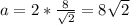 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
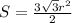 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

Объяснение:
7tg^2 x + 3tg x + 2cos^2 x - 7cos x + 1 = 0
Можно применить универсальную тригонометрическую подстановку.
t = tg(x/2), тогда 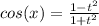 ,
, 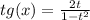 . Подставляем:
. Подставляем:
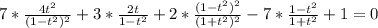
Приводим к общему знаменателю (1-t^2)^2*(1+t^2)^2:

Избавляемся от дробей:
28t^2(1+2t^2+t^4) + 6(t-t^3)(1+2t^2+t^4) + 2(1-2t^2+t^4)(1-2t^2+t^4) -
- 7(1+t^2)(1-3t^2+3t^4-t^6) + (1-2t^2+t^4)(1+2t^2+t^4) = 0
Раскрываем скобки:
28t^2 + 56t^4 + 28t^6 + 6t - 6t^3 + 12t^3 - 12t^5 + 6t^5 - 6t^7 + 2 - 4t^2 + 2t^4 -
- 4t^2 + 8t^4 - 4t^6 + 2t^4 - 4t^6 + 2t^8 - 7 - 7t^2 + 21t^2 + 21t^4 - 21t^4 - 21t^6
+ 7t^6 + 7t^8 + 1 - 2t^2 + t^4 + 2t^2 - 4t^4 + 2t^6 + t^4 - 2t^6 + t^8 = 0
Приводим подобные:
t^8*(2+7+1) - 6t^7 + t^6*(28-4-4-21+7+2-2) - 6t^5 + t^4*(56+2+8+2+21-21+1-4+1)
+ 6t^3 + t^2*(28-4-4-7+21-2+2) + 6t + (2-7+1) = 0
10t^8 - 6t^7 + 6t^6 - 6t^5 + 66t^4 + 6t^3 + 34t^2 + 6t - 4 = 0
Делим все на 2
5t^8 - 3t^7 + 3t^6 - 3t^5 + 33t^4 + 3t^3 + 17t^2 + 3t - 2 = 0
Это уравнение имеет 2 иррациональных корня:
t1 = tg(x/2) ≈ -0,387
x/2 ≈ -arctg(0,387) + П*k
x1 ≈ -2arctg(0,387) + 2П*k, k ∈ Z
t2 = tg(x/2) ≈ 0,25
x/2 ≈ arctg(0,25) + П*k
x2 ≈ 2arctg(0,25) + 2П*k, k ∈ Z
В общем, у меня такое чувство, что в задании опечатка.
Слишком сложно получилось.
Ну, или это задание из математической спецшколы.
а) нет (в задаче проценты брака меньше 1)
б) можно брать сколько угодно деталей, но разница не станет равна 4%, так как они делают браки в процентах от количества деталей, поэтому как не меняй количество деталей процент брака останется тот же