3. 
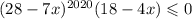
Заметим, что так как 2020 - четное число, то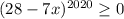 
(число в четной степени всегда 
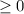). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если 
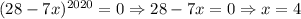, то имеем : 
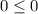, а это верно. Поэтому нужно запомнить , что x = 4 - решение.
Если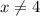 
, то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
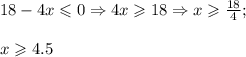
Решение неравенства - x = 4 и все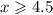 
. Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
ОТВЕТ: 1) 120.
4. Область определения - все числа, которые можно подставить вместо x.
Под каждым из корней должно быть неотрицательное число, а знаменатель дроби должен быть отличен от 0. Область определения - все числа, удовлетворяющие системе из четырех неравенств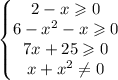 
.
Из первого неравенства следует, что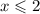 
.
Решим второе неравенство: оно равносильно неравенству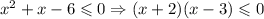 
. Решением данного неравенство является отрезок [-2; 3].
Третье неравенство: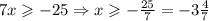 
.
Четвертое: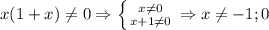 
Так как у нас была система, ищем пересечение множеств решений всех 4 неравенств: ![x\in[-3;-1)\cup(-1;0)\cup(0;2].](/tpl/images/1359/4742/04668.png)
Все целые числа, принадлежащие области определения: -3; -2; 1; 2 (-1 и 0 выпадают, т.к. скобки круглые). Их сумма равна -2.
ОТВЕТ: 2) -2
3.
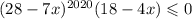
Заметим, что так как 2020 - четное число, то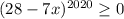
(число в четной степени всегда 
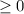). Поэтому первый множитель на знак левой части влиять не будет и его можно опустить. При этом стоит учесть, так это то, что если 
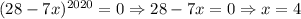, то имеем : 
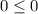, а это верно. Поэтому нужно запомнить , что x = 4 - решение.
Если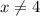
, то первый множитель положителен и на него можно поделить обе части, сохранив знак. Итого:
Решение неравенства - x = 4 и все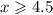
. Наименьшие целые решения - 4, 5 и 6. Их произведение равно 120.
ОТВЕТ: 1) 120.
4. Область определения - все числа, которые можно подставить вместо x.
Под каждым из корней должно быть неотрицательное число, а знаменатель дроби должен быть отличен от 0. Область определения - все числа, удовлетворяющие системе из четырех неравенств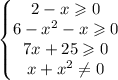
.
Из первого неравенства следует, что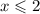
.
Решим второе неравенство: оно равносильно неравенству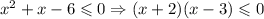
. Решением данного неравенство является отрезок [-2; 3].
Третье неравенство: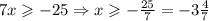
.
Четвертое: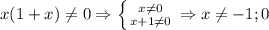
Так как у нас была система, ищем пересечение множеств решений всех 4 неравенств:![x\in[-3;-1)\cup(-1;0)\cup(0;2].](/tpl/images/1359/4742/04668.png)
Все целые числа, принадлежащие области определения: -3; -2; 1; 2 (-1 и 0 выпадают, т.к. скобки круглые). Их сумма равна -2.
ОТВЕТ: 2) -2