
a) Найдём точки пересечения графика ф-ции с осью ОУ, для этого надо положить х=0.

Точка пересечения графика с ОУ - точка А(0; -5) .
б) Найдём точки пересечения графика ф-ции с осью ОХ, для этого надо положить у=0.
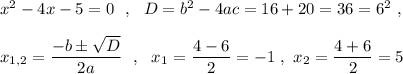
Точки пересечения графика с ОХ - точки В(1-;0) и С(5;0) .
в) Ось симметрии заданной параболы проходит через её вершину перпендикулярно оси ОХ . Найдём абсциссу вершины параболы.
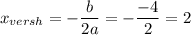
Ось симметрии - прямая х=2 .
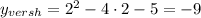 , координаты вершины параболы V(2;-9) .
, координаты вершины параболы V(2;-9) .
c) Для построения графика, можно найти координаты точки, симметричной точке А(0;-5) относительно оси х=4. Это точка D(4;-5) .
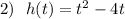
Графиком заданной функции является парабола с ветвями , направленными вверх, так как коэффициент перед t² равен 1>0 . А если ветви у параболы направлены вверх, то траектория движения не соответствует движению подброшенного мяча . Поэтому условие задано некорректно .
уравнение с параметром просто как и в обыкновенном кв. уравнинии вот найди дискриминант и корни уравн
дискриминант=4a^2-4(a-2)(2-3a)=4a^2-4(2a-3a^2-4+6a)=4a^2-8a+12a^2+16-24a=16a^2-32a+16=(4a-4)^2
-2a+корень из (4a-4)^2 -2a+4a-4 2a-4
x1====1
2(a-2) 2a-4 2a-4
первый корень x1=1
-2a-корень из (4a-4)^2 -2a-4a+4 -6a+4 2(-3a+2) 2-3a
x2=== =
=
2(a-2) 2(a-2) 2(a-2)
Объяснение:
У=х^2-4х-5
а)
Х=0
У=0^2-4×0-5= - 5
(0;-5) точка пересечения с осью Оу
б)
У=0
0=х^2-4х-5
Х^2-4х-5=0
D=(-4)^2-4×1×(-5)=16+20=36
X1=(4-6)/2= - 1
X2=(4+6)/2=5
(-1;0) (5;0) точки пересечения с осью 0Х
в)
Х= - b/2a
X= - (-4)/2×1=2
X=2 ось симметрии
с)
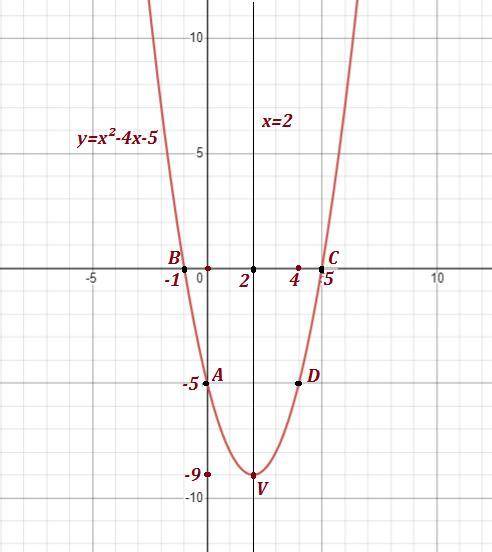
График на фото
Х 0 1 2 3 4
У - 5 - 8 - 9 - 8 - 5
2
h(t)=t^2-4t
Ветви параболы направлены вверх,
условие не корректно.