Легко заметить, что оба уравнения имеют корни x=±1
Уравнение 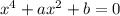
имеет корни: x=±1
значит
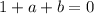 ⇒
⇒ 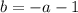
Уравнение принимает вид:
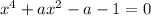
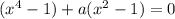
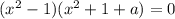
Третий корень только
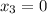
при 
Тогда
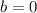
Уравнение 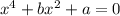
при  и
и 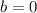
принимает вид:
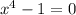
и имеет два корня x=±1
Вынесем общий множитель cos x
cos x(sin в квадрате x-4sin x+cos в квадрате х)=0
cos x=0 или (4*sin в квадрате x-4sin x+cos в квадрате х)=0
x=Пn. где n принадлежит z. Во втором уравнении cos в квадрате x заменяем на 1-sin в квадрате х
4*sin в квадрате x-4sin x+1-sin в квадрате х=0
3sin в квадрате х-4*sin x +1=0
Пусть у=sin x
3y в квадрате х+4y+1=0
Решим квадратное уравнение с дискриминанта, получим
у1=1
y2=1/3
sin x=1. x=П/2+2Пn.где n принадлежит z
sin x=1/3. x=(-1)^n arc sin 1/3 +Пn.где n принадлежит z
ответ:x=Пn. где n принадлежит z;
x=П/2+2Пk.где k принадлежит z
x=(-1)^r arc sin 1/3 +Пr.где r принадлежит z
1) Дано: 2^(5x-1)+2^(5x-2)+2^(5x-3)=896
Делаем преобразование левой части уравнения: 2^(5x-1)+2^(5x-2)+2^(5x-3) = 7*2^(5x-3)
Уравнение после преобразования: 7*2^(5x-3) = 2^7 * 7
Упрощаем: 2^(5x-1)+2^(5x-2)+2^(5x-3) - 896 = 0
ответ (решение уравненияс учётом ОДЗ): нет действительных решений.
2) Дано: 5^(2*x-1)+2^2*x = 5^2*x-2^(2*x+2)
Делаем преобразование левой части уравнения: 5^(2*x-1)+2^2*x = (5^2*x+20x)/5
Делаем преобразование правой части уравнения: 5^(2*x) - 2^(2*x+2) = -(2^(2*x+2) - 25x)
Уравнение после преобразования: (5^2*x+20x)/5 = -(2^(2*x+2) - 25x)
Приводим подобные: 5^(2*x-1) + 4x = 25x - 2^(2*x+2)
Упрощаем: 2^(2*x+2) + 5^(2*x-1) - 21x = 0
Возможные решения: 1
ответ(решение уравнения с учётом ОДЗ): 1.
2 корня
Объяснение:
x⁴+ax²+b=0
Данное уравнение является биквадратным и должно иметь 4 корня. По условию, оно имеет три корня, т.е. три действительных корня. При b=0 это возможно.
Покажем это:
Замена: x²=y
y²+ay+b=0
При b=0 y²+ay=0
y(y+a)=0
y=0 или y+a=0
y=-a
Обратная замена: y=x²
x²=0 или x²= -a
x₁=0 x₂=√-a x₃=-√-a
Итак, уравнение x⁴+ax²+b=0 имеет три корня
При b=0 уравнение x⁴+bx²+a=0 при b=0 преобразуется в уравнение
x⁴+a=0
x⁴= -a
Получаем, что это уравнение имеет два корня