Формула сложной процентной ставки: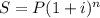 
, где S - наращенная сумма, P - первоначальная сумма вклада, i - процентная ставка, n - срок ссуды;
Само решение:
Пусть клиент сначала положил x грн в банк, тогда через год он получит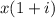 
грн и получил он прибыль 100 грн, т.е. 
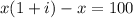откуда 
К общей сумме он добавил 400 грн на год свои сбережения в банке, то на следующий год он получит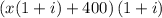 
грн, что по условию вклад вместе с процентами составил 1650 грн.
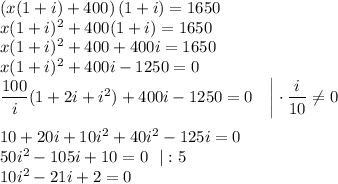
Решаем как квадратное уравнение через дискриминант
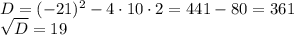
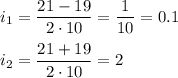
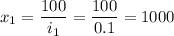грн - начальная сумма вклада
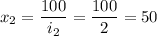грн - не подходит условию, так как клиент положил несколько 100 гривневых купюр
ответ: начальная сумма вклада 1000 грн с 10% годовыми.
R = 3 м
искомая площадь S это площадь круга за вычетом площади квадрата
S = S(круга) - S(квадрата)
S(круга) = π·R²,
Чтобы найти площадь квадрата, найдём сначала сторону квадрата a. Т.к. прямой вписанный угол квадрата опирается на диаметр, тогда по теореме Пифагора найдём
(2R)² = a² + a²
2a² = 4R²
a² =2R²
Площадь квадрата = a² = 2R²
S = πR² - 2R²
S = 3²·(π - 2) м² = 9·(π - 2) м²