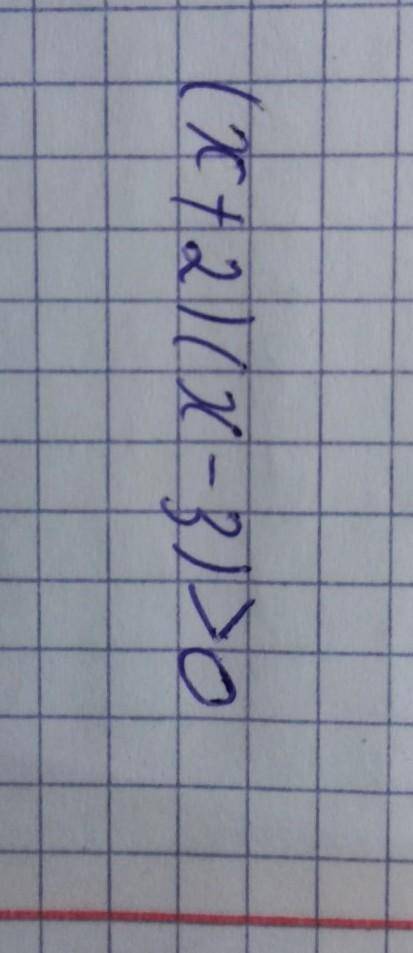
Объяснение:
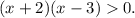
-∞__+__-2__-__3__+__+∞ ⇒
ответ: x∈(-∞;-2)U(3;+∞).
Объяснение:
a) x² - 2x - 15 < 0
x² + 3x - 5x - 15 > 0
x(x + 3) - 5(x + 3) > 0
(x + 3)(x - 5) > 0
x + 3 < 0 x - 5 > 0
x < -3 x > 5
x ∈ (-∞, -3) ∪ (5, +∞)
б) -x² + 6x ≥ 0
-x(x - 6) ≥ 0
x(x - 6) ≤ 0
x ≥ 0 x - 6 ≤ 0
x ≤ 6
x ∈ [0, 6]
в)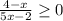 
4 - x ≤ 0 5x - 2 > 0
x ≤ 4 5x > 2
x >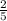 
x ∈ (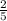, 4]
г) x(x - 9)(x + 2) > 0
x < 0 (x - 9)(x + 2) > 0
x - 9 > 0 x + 2 > 0
x > 9 x > -2
x ∈ (-2, 0) ∪ (9, +∞)
д)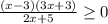 
2x + 5 > 0 (x - 3)(3x + 3) ≥ 0
2x > -5 x - 3 ≥ 0 3x + 3 ≤ 0
x >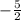 
x ≥ 3 3x ≤ -3
x ≤ -1
x ∈ (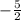 , -1] ∪[3, +∞)
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2
Объяснение:
Решить систему уравнений
(x-5y)(x²-36)=0
x-y=4
Выразим х через у во втором уравнении:
х=4+у
Первые скобки приравняем к нулю, как один из множителей, дающих в результате ноль:
x-5y=0
Подставим выраженное х через у:
4+у-5у=0
4-4у=0
-4у= -4
у= -4/-4
у₁=1
Теперь подставляем значение у в уравнение первых скобок и вычисляем х:
x-5y=0
х=5у
х=5*1
х₁=5
Теперь приравняем к нулю вторые скобки, как один из множителей, дающих в результате ноль:
x²-36=0
x²=36
х₂,₃=±√36
х₂= -6
х₃=6
x-y=4
-у=4-х
у=х-4
у₂=х₂-4
у₂= -6-4
у₂= -10
у₃=х₃-4
у₃=6-4
у₃=2
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2
решение смотри на фотографии