Решение.
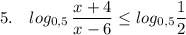
ОДЗ: выражение под знаком log строго больше 0 ,
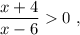 знаки: (-4) - - - - - (6)
знаки: (-4) - - - - - (6) 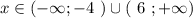
Основание логарифма 0<0,5<1 , поэтому это убывающая функция, и знак между аргументами логарифмической функции будет противоположным .
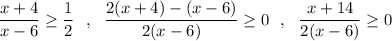
знаки: [-14] - - - - (6) ![x\in (-\infty ;-14\, ]\cup (\ 6\ ;+\infty )](/tpl/images/4906/5028/6865a.png)
C учётом ОДЗ ответ: ![x\in (-\infty ;-14\, ]\cup (\ 6\ ;+\infty )](/tpl/images/4906/5028/6865a.png) .
.
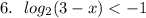
ОДЗ: 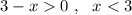
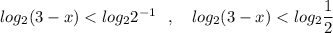
Логарифмическая функция с основанием 2>1 возрастающая, поэтому знак между аргументами логарифмической функции будет таким же .
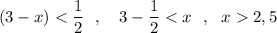
Учтём ОДЗ: 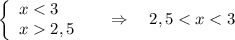
ответ: 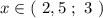 .
.
Решение на фотографии