Question

2x+4y+3z=-10 -x+5y-2z=5 3x-2y+4z=3 методом крамера, 7 задания второй пример

Answer 1

ответ:  $\displaystyle \left(\frac{113}{5} ;\;-\frac{6}{5} ;\;-\frac{84}{5}\right)$

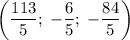
Объяснение:

Решить систему методом Крамера:

$\begin{equation*} \begin{cases} 2x+4y+3z=-10 \\-x+5y-2z=5 \\3x-2y+4z=3 \\ \end{cases}\end{equation*}$

Найдем главный определитель системы:

$\Delta=\begin{vmatrix} a_1& b_1&c_1\\ a_2 &b_2&c_2\\a_3& b_3&c_3\\\end{vmatrix}$

где a, b, c - числовые коэффициенты при x, y, z соответственно.

Найдем определитель разложением по первой строке:

Δ = a₁ · (b₂c₃ - b₃c₂) - b₁ · (a₂c₃ - a₃c₂) + c₁ · (a₂b₃ - a₃b₂)

Вычислим Δ:

$\displaystyle \Delta=\begin{vmatrix} 2& 4&3\\ -1 &5&-2\\3& -2&4\\\end{vmatrix}==2(5\cdot4-(-2)\cdot(-2))-4((-1)\cdot4-3\cdot(-2))+3((-1)\cdot(-2)-3\cdot5)==32-8-39=-15$

Δ ≠ 0 ⇒ система имеет единственное решение.

Для нахождения корней необходимо вычислить еще три определителя:

1. Δх.

Заменим в главном определителе первый столбец на столбец свободных членов (d):

$\Delta_x=\begin{vmatrix} d_1& b_1&c_1\\ d_2 &b_2&c_2\\d_3& b_3&c_3\\\end{vmatrix}$

Вычислим Δх:

$\displaystyle \Delta_x=\begin{vmatrix} -10& 4&3\\ 5 &5&-2\\3& -2&4\\\end{vmatrix}==-10\cdot(5\cdot4-(-2)\cdot(-2))-4\cdot(5\cdot4-3\cdot(-2))+3\cdot(5\cdot(-2)-3\cdot5)==-160-104-75=-339$

2. Δy.

Заменим в главном определителе второй столбец на столбец свободных членов (d):

$\Delta_y=\begin{vmatrix} a_1& d_1&c_1\\ a_2 &d_2&c_2\\a_3& d_3&c_3\\\end{vmatrix}$

Вычислим Δy:

$\displaystyle \Delta_y=\begin{vmatrix} 2& -10&3\\ -1 &5&-2\\3& 3&4\\\end{vmatrix}==2\cdot(5\cdot4-3\cdot(-2))+10\cdot((-1)\cdot4-3\cdot(-2))+3\cdot((-1)\cdot3-3\cdot5)==52+20-54=18$

3. Δz.

Заменим в главном определителе третий столбец на столбец свободных членов (d):

$\Delta_z=\begin{vmatrix} a_1& b_1&d_1\\ a_2 &b_2&d_2\\a_3& b_3&d_3\\\end{vmatrix}$

Вычислим Δz:

$\displaystyle \Delta_z=\begin{vmatrix} 2& 4&-10\\ -1 &5&5\\3& -2&3\\\end{vmatrix}==2\cdot(5\cdot3-(-2)\cdot5)-4\cdot((-1)\cdot3-3\cdot5)-10\cdot((-1)\cdot(-2)-3\cdot5)==50+72+130=252$

ответ рассчитывается по формулам:

$\displaystyle x=\frac{\Delta_x}{\Delta} ;\;\;\;\;\; y=\frac{\Delta_y}{\Delta} ;\;\;\;\;\; z=\frac{\Delta_z}{\Delta}$

Найдем корни:

$\displaystyle x=\frac{-339}{-15}=\frac{113}{5} ;\;\;\;\;\; y=\frac{18}{-15}=-\frac{6}{5} ;\;\;\;\;\; z=\frac{252}{-15}=-\frac{84}{5}$

ответ:  $\displaystyle \left(\frac{113}{5} ;\;-\frac{6}{5} ; \;-\frac{84}{5}\right)$

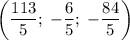
#SPJ1