Круглые скобки пишут в строгих неравенствах и на концах отрезков с выколотыми точками (<,> - строгие знаки) Квадратные скобки пишут в нестрогих неравенствах в случае закрашенных точек (≤,≥≥ - нестрогие знаки) если требуемый интервал является крайним слева то нужно писать -∞, если крайним справа то нужно написать +∞ Пример в файле т.к. по условию требуются значения меньше или равно 0, то берем те интервалы где знак "-" первый интервал является крайним слева, поэтому нужно написать (-∞;-2], при этом у тройки скобка квадратная, т.к. знак неравенства нестрогий и -2 это ноль числителя второй интервал (0;3] в этом случае у 0 стоит крглая скобка т.к. х=0 - это ноль знаменателя и в область значения неравенства не входит, а у 3 скобка опять квадратная потому что х=3 - ноль числителя и знак неравенства нестрогий
.Я вам У меня с этим твёрдо. Первое правило:бесконечность всегда в круглых скобках.(это связано с тем,что неизвестно,какой аргумент мы возьмём). Когда бесконечность?Да когда неизвестно,о каком наибольшем значении идёт речь.Например,х>4 (4;+∞) Спросите,почему при 4 круглая скобка. Объясняю.Когда мы решаем неравенство,мы разбиваем область определения функции НУЛЯМИ ФУНКЦИИ на промежутки знакопостоянства,0 же нам никакого знака не даёт,правильно,вот и брать его нельзя. А вот когда вам встречается значок≥,значит,вы имеете право взять ноль,в таком случае берёте 4 в квадратных скобках.Т.е.,запомните правило,квадратная скобка - граница,возможность схватить нуль. ВОт и вся теория!Но зависит от конкретного случая,конечно.
ответ: 2,2 ; 0,4 ; -1,4 ; -3,2 .
Задана арифметическая прогрессия: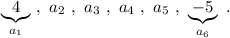
Формула n-го члена арифм. прогрессии: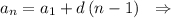
Каждый последующий член арифм. прогрессии отличается от
предыдущего на число, равное . Поэтому вычислим
. Поэтому вычислим
неизвестные члены арифм. прогрессии, пользуясь этим свойством.