Заданы две точки с координатами : (2 ; 1) и (0 ; 2) .
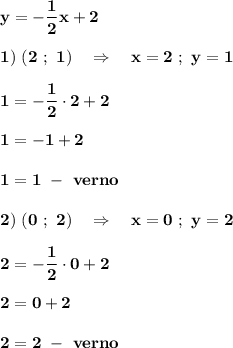
ответ : Д
x^2+y^2+2xy+4(x+y)=27
(x+y)^2+4(x+y)+4=31
((x+y)+2)^2=(sqrt(31))^2
(x+y)=-2+sqrt(31) x+y=-2-sqt(31)
1) (x-y)^2-4(x+y)=7
(x-y)^2=7-8+4*sqrt(31)=4*sqrt(31)-1
x-y=sqrt(4*sqrt(31)-1) x-y=-sqrt(4*sqrt(31)-1)
a) x=1+(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
y=1-(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
b) x=1-(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
y=1+(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
2) вариант x+y=-2-sqt(31)
невозможен, т.к. тогда (х-у)^2<0
ответ : два решения
a) x=1+(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
y=1-(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
b) x=1-(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
y=1+(sqrt(31)+ sqrt(4*sqrt(31)-1))/2
"Красивого" ответа с этими числами нет.
Если нужно выбрать верны утверждения, то это 2 и 4.
Смотрим, белый короче желтого, но длиннее синего.
Расположим шарфы в порядке уменьшения их длины, получаем:
Желтый, белый, синий. Читаем далее, черный не длиннее белого, следовательно, он может быть как равен по длине, так и меньше.
Тогда примерное расположение шарфов:
Желтый, белый, синий и черный(черный и синий могут меняться местами в зависимости от их длины)
Смотрим утверждение, 1 не верно, так как черный шарф может быть как равен по длине, так и меньше.
2 утверждение верно, так как читая условие делаем вывод, что желтый длиннее всех(см. выше).
3 утверждение не верно, так как в условии сказано, что белый шарф длиннее.
4 утверждение верно, так как желтый шарф самый длинный.
Объяснение:
На графике изображены точки с координатами (0;2) и (2;1)
Надо координаты этих точек подставить последовательно в каждую функцию и если равенство будет верным, то график функции проходит через точки.
А) у=-2х+2
Подставляем координаты точки (0;2):
2 = -2•0+2
2 = 2 - равенство верное. График этой функции проходит через точку (0;2)
Подставляем координаты точки (2;1):
1 = -2•2+2
1 = -2 - равенство неверное. График этой функции не проходит через точку (0;2)
Б) у=2х+2
Подставляем координаты точки (0;2):
2 = 2•0 +2
2 = 2 - равенство верное. График этой функции проходит через точку (0;2)
Подставляем координаты точки (2;1):
1 = 2•2+2
1 = 6 - равенство неверное. График этой функции не проходит через точку (0;2)
В) у=-х+2
Подставляем координаты точки (0;2):
2 = 0 +2
2 = 2 - равенство верное. График этой функции проходит через точку (0;2)
Подставляем координаты точки (2;1):
1 = -2+2
1 = 0 - равенство неверное. График этой функции не проходит через точку (0;2)
Д) у= - ½•х+2
Подставляем координаты точки (0;2):
2 = - ½ • 0 +2
2 = 2 - равенство верное. График этой функции проходит через точку (0;2)
Подставляем координаты точки (2;1):
1 = - ½ •2+2
1 = 1 - равенство верное. График этой функции проходит через точку (0;2)
Так как график этой функции проходит через обе эти точки, то это и есть наш ответ: Д