x³ - 18x² + 95x - 126 = (x-2) · x³ - 18x² + 95x - 126 / (x-2)
x³ - 18x² + 95x - 126 / x-2 = x² - 16x + 63 = (x-2)·(x² - 16x + 63) = (x-2)·(x-7)·(x-9)
1. Построить график. Находим вершину параболы. Приводим к виду:
y = x² - 6*x +5 = (x² - 2*x*3 + 3²)-9 +5 = (x-3)² - 4
Получили уравнение ОБЫЧНОЙ ПАРАБОЛЫ ИКС КВАДРАТ, но с вершиной в точке А(3;-4)
Решив уравнение получаем нули функции - х1 = 1 и х2 = 5.
Рисунок с графиком к задаче в приложении.
ответы на вопросы:
1) У(0,5) = 1/4 - 6*0,5 +5 = 2,25 - ответ
2) Y(x) = -1
Решаем квадратное уравнение
x² - 6x - 6 = 0 и получаем: х1 ≈ 1,3 и х2 ≈ 4,7. (с ГРАФИКА).
Интервалы знакопостоянства.
Y>0 - X∈(-∞;-1]∪[5;+∞) - положительна.
Y<0 - X∈[-1;5] - отрицательна.
Внимание - важно. Функция непрерывная - квадратные скобки в написании интервалов у нулей функции.
Решив уравнение получаем нули функции - х1 = 1 и х2 = 5.
4. Возрастает после минимума - Х∈[3; +∞)
и убывает при Х∈(-∞;3]
Объяснение:
незачто!
Объяснение:
сначала считаем то, что в скобках, там у нас 4/9 + 15/18. чтобы сложить дроби, надо чтобы в знаменателе было одно и тоже число (сверху в дроби числитель, а снизу знаменатель). значит... чтобы у этих дробей знаменатель был одинаковый, нужно найти НОК знаменателей этих дробей... тоесть НОК 18 и 9... думаю ты умеешь это делать, получится 18. далее, в правой дроби у нас знаменатель уже =18, значит ничего не делаем, и оставляем как есть, а в первой дроби нужно знаменатель умножить на 2. (ну 18 это 9 умножить на 2). НО умножать только знаменатель нельзя! нужно ещё и числитель умножить на это число. значит, 4/9 будет равно 8/18, теперь складываем дроби. 8/18 + 15/18 = 23/18
дальше...
нам нужно 18/7 × 23/18...
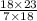
18 сверху и снизу сокращеются... получается
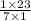
тоесть просто 23/7
теперь выделяем целую часть... и получаем дробь
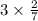
*записывать без знака умножения!*
ответ: ( х - 2 ) × ( х - 7 ) × ( х - 9 )
х³ - 18х² + 95х - 126
х³ - 2х² - 16х² + 32х + 63х - 126
х² × ( х - 2 ) - 16х × ( х - 2 ) + 63 ( х - 2 )
( х - 2 ) × ( х² - 16х + 63 )
( х - 2 ) × ( х² - 7х - 9х + 63 )
( х - 2 ) × ( х × ( х - 7 ) - 9 ( х - 7))
( х - 2 ) × ( х - 7 ) × ( х - 9 )