Биквадратное уравнение.
Решается заменой переменной:

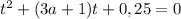
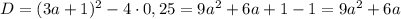
Если D >0, т.е.


уравнение имеет корни:
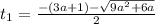 или
или 
Обратный переход:
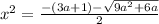 или
или 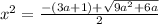
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
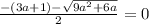
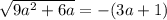
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
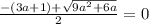
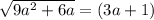
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 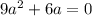
 или
или 
При 
уравнение принимает вид:

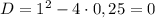 ⇒
⇒ 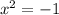
уравнение не имеет корней
При 
уравнение принимает вид:

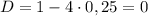 ⇒
⇒ 
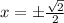
Уравнение 4-ой степени, значит
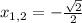 и
и 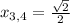
О т в е т. При 
разница арифметичесской прогрессии равна
d=a[2]-a[1]=4.2-4.6=-0.4
общий член арифметичесской прогрессии равен
a[n]=a[1]+d*(n-1)
a[n]=4.6-0.4*(n-1)=4.6-0.4n+0.4=5-0.4n
найдем сколько положительных членов в данной арифметичесской прогрессии
5-0.4n>0
-0.4n>-5
n<5:0.4
n<12.5
12 наибольшее натуральное число, удовлетворяющее неравенство
значит первые 12 членов данной арифметичесской прогрессии положительные
Сумма первых n членов арифметической прогресси равна
S[n]=(2*a[1]+(n-1)*d)/2*n
S[12]=(2*4.6+(12-1)*(-0.4))/2*12=28.8
отвте: 28.8
72 км/ч.
Объяснение:
Пусть скорость грузового автомобиля х км/ч, тогда скорость легкового х+12 км/ч. (3 минуты=1/20 часа)
18/х - 18/(х+12) = 1/20
360х+4320-360х-х²-12х=0
х²+12х-4320=0
По теореме Виета х=-72 (не подходит) х=60.
Скорость легкового автомобиля 60+12=72 км/ч.