Объяснение:
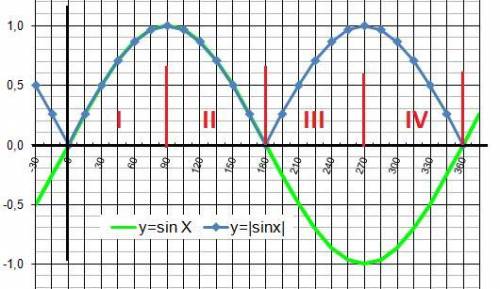
1) Если |sin a| = sin a, то sin a > 0, a ∈ 1 или 2 четверти
2) Если |sin a| > sin a, то sin a < 0, |sin a| > 0, a ∈ 3 или 4 четверти
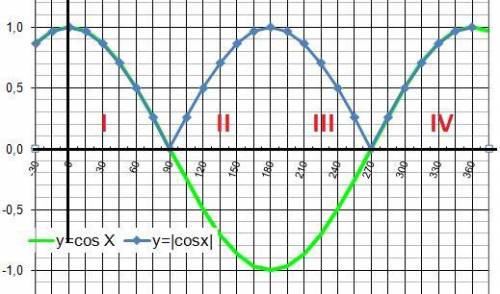
3) Если |cos a| = cos a, то cos a > 0, a ∈ 1 или 4 четверти
4) Если |cos a| > cos a, то cos a < 0, |cos a| > 0, a ∈ 2 или 3 четверти
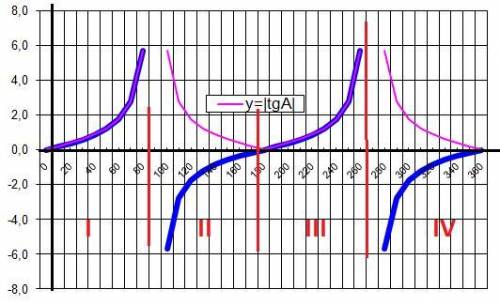
5) Если |tg a| = tg a, то tg a > 0, a ∈ 1 или 3 четверти
6) Если |tg a| > tg a, то tg a < 0, |tg a| > 0, a ∈ 2 или 4 четверти
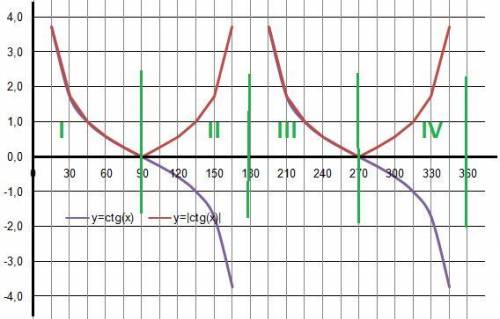
7) Если |ctg a| = ctg a, то ctg a > 0, a ∈ 1 или 3 четверти
8) Если |ctg a| > ctg a, то ctg a < 0, |ctg a| > 0, a ∈ 2 или 4 четверти
Объяснение:
Рисунки к вопросу в приложениях.
Задача 21.11 В какой координатной четверти может находиться угол.
1) |sinα| = sinα - в I и II четвертях окружности.
2) |sinα| > sinα - в III и IV четвертях окружности.
3) |cosα| = cosα - в I и IV четвертях окружности.
4) |cosα| > cosα - во II и III четвертях окружности.
5) |tgα| = tgα - в I и III четвертях окружности.
6) |tgα| > tgα - в II и IV четвертях окружности.
7) |ctgα| = ctgα - в I и IIII четвертях окружности.
8) |ctgα| > ctgα - во II и IV четвертях окружности.
Відповідь: 204 .
Пояснення:
→ k=(- 1 ; 4 ) ;→m=( 3 ; 5 ) ;
Вектори 3k = 3* (- 1 ; 4 ) = (- 3 ; 12 ) ; 4m = 4* ( 3 ; 5 ) = ( 12 ; 20 ) .
Скалярний добуток векторів ( 3k ) * ( 4m ) = - 3 * 12 + 12 * 20 =
= - 36 + 240 = 204 .