Рассмотрим сначала особую точку --- там парабола вырождается в прямую. Тогда
Значит, все дальнейшие рассуждения проводим при .
Найдём корни функции :
где --- вершина параболы и по совместительству точка экстремума функции .
Значение функции в этой точке равно
Из исследования знаков производной/функции легко установить, что при величина --- максимум (это, впрочем, понятно и из вида функции ), больший нуля. Причём в этом случае , т.е. понятно, что в области функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения .
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим .
Корни и точка экстремума:
Теперь уже - минимум функции, а (после аналогичного анализа) .
Если нам повезёт, то правый (который ) корень будет лежать левее точки , а это будет означать, что к тому времени как функция подойдёт к , она уже будет положительна (ведь правее экстремума парабола рогами вверх будет идти только вверх). Исследуем:
Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов: Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.
Как решать квадратные уравнения? Смотри. Уравнение: ах^2+bx+c=0 называется квадратным. Например, х^2-х-6=0 Решается оно через дискриминант. Точное определение дискриминанта, к сожалению, дать не смогу. Находится он по формуле: b^2-4ac. Найдём дискриминант нашего уравнения: Д=(-1)^2-4*1*(-6)=1+24=25. А теперь нам предстоит найти корни уравнения. В квадратном уравнении, как правило, их 2. Реже - 1 корень, или вовсе корней нет. Всё зависит от дискриминанта. Если он больше нуля - то 2 корня, и формула: х_1,2=(-b(+-)√Д) / 2а. Если дискриминант равен 0, то 1 корень, и формула: х=-b/2a. А если дискриминант меньше нуля - то корней нет. Найдём корни нашего уравнения: Их у нас два, так как дискриминант больше нуля: х_1,2=(1+-√25)/2=(1+-5)/2. Это формула двух корней. А теперь найдём каждый корень по отдельности: х_1=(1+5)/2=6/2=3; х_2=(1-5)/2=-4/2=-2. Корнями будут являться числа 3 и -2. Итак, запишем теперь ответ: х_1=3; х_2=-2.
Всё просто! Со временем ты будешь щелкать эти уравнения, как семечки! ;)
А решение твоих уравнений находится во вложении, только там кратко, не запутайся)
Рассмотрим сначала особую точку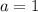 --- там парабола вырождается в прямую. Тогда
--- там парабола вырождается в прямую. Тогда
Значит, все дальнейшие рассуждения проводим при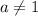 .
.
Найдём корни функции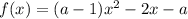 :
:
где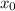 --- вершина параболы и по совместительству точка экстремума функции
--- вершина параболы и по совместительству точка экстремума функции 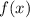 .
.
Значение функции в этой точке равно
Из исследования знаков производной/функции легко установить, что при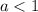 величина
величина 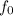 --- максимум (это, впрочем, понятно и из вида функции
--- максимум (это, впрочем, понятно и из вида функции 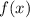 ), больший нуля. Причём в этом случае
), больший нуля. Причём в этом случае  , т.е. понятно, что в области
, т.е. понятно, что в области 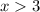 функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
функция будет падать от какого-то максимального положительного (это в лучшем случае, а может уже и от отрицательного) значения. В любом случае, рано или поздно значение функции станет меньше нуля.
Таким образом, рассматриваем значения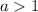 .
.
Ну, раз просят наименьшее целое значение параметра, то не будем далеко ходить и рассмотрим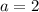 .
.
Корни и точка экстремума:
Теперь уже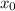 - минимум функции, а (после аналогичного анализа)
- минимум функции, а (после аналогичного анализа) 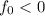 .
.
Если нам повезёт, то правый (который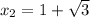 ) корень будет лежать левее точки
) корень будет лежать левее точки 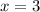 , а это будет означать, что к тому времени как функция подойдёт к
, а это будет означать, что к тому времени как функция подойдёт к 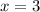 , она уже будет положительна (ведь правее экстремума
, она уже будет положительна (ведь правее экстремума 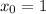 парабола рогами вверх будет идти только вверх). Исследуем:
парабола рогами вверх будет идти только вверх). Исследуем:
Победа.
ответ.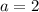 .
.