***
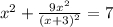 =>
=> 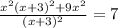 =>
=> 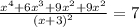
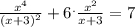
пусть:
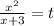
используя теорему Виета
находим t1 и t2
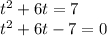
=>
t₁ = -7
t₂ = 1
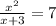 =>
=> 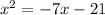 =>
=> 
находим дискриминант уравнения х² + 7х + 21 = 0
D = b² - 4ac = 49 - 4 · 1 · 21 = 49 - 84 = - 35 < 0
поскольку дискриминант отрицательный, значит уравнения не имеет решений
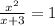 =>
=> 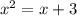 =>
=> 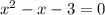
находим дискриминант уравнения х² - х - 3 = 0
D = b² - 4ac = (-1)² - 4 · 1 · (-3) = 13
X₁ = (-b + √D) / 2 = (1 + √13) / 2X₂ = (-b - √D) / 2 = (1 - √13) / 2ответ: X₁ = (-b + √D) / 2 = (1 + √13) / 2
X₂ = (-b - √D) / 2 = (1 - √13) / 2
|| - параллельнсть
l - переменная
k - коэффициент
функции ||, если они не могут быть равны, т.е. у них нет точек пересечения, согласно определению параллельности (|| те прямые, которые не имеют точек пересечения).
а если точка пересечения есть, тогда функции пересекаются, т.е. они оба пересекают определенную координату, следовательно они должны быть равны между собой
линейные функции
тогда можно прийти к выводу, что если k1=k2, функции параллельны, ибо:
y=kx+l если представить как равно значение:
kx+l=kx+l
l=l, т.е. если k1=k2, l1=l2, проще говоря, не существует какой-либо функции, которая пересекает y=kx+l, если их k равны.
например, y=5x+2
5x+2=5x+2
2=2, если вместо 2 мы подставим любое другое число, равенство станет неверным.
из этого можно сделать вывод, что если k1 не равно k2, тогда функции пересекаются, ибо:
y=k1x + l и y=k2x+l
k1x + l = k2x+ l
l мы сможем сократить только при условии, что они равны, но тогда мы получим все равно верное равенство, просто тогда точкой пересечения будет (0; l), т.е. при x=0 функции станут равными, ибо при умножении k на 0 будет 0, останется только l=l
если же l1 не равно l2, тогда у нас выйдет уравнение с 2 переменными, а значит оно имеет бесконечное множество решений при любом х (если, конечно, x имеет смысл и нет всяких делений на 0 и т.д.), следовательно первая функция при любых значениях k и l будет иметь точку пересечения со второй функцией, если k второй функции не равен k первой функции
1 || 2 || 3
ответ: 7±√70.
Объяснение:
x^2+9*x^2/(x+3)^2=7;
10x²/x²+6x+9=7;
10x²=7x²+42x+63;
3x^2-42x-63=0;
x²-14x-21=0;
a=1; b=-14; c=-21;
D=b²-4ac=196-4*1*(-21)=196+84=280>0-2 корня
x1.2=(-b±√D)/2a=(-(-14)±√280)/2*1=(14±2√70)/2=7±√70;