Наименьший положительный период функции равен 1. При прибавлении или отнимании числа от аргумента график функции смещается влево или вправо вдоль оси абсцисс, таким образом это действие не оказывает влияния на длину периода. С умножением аргумента на коэффициент функция «пробегает» этот период в такое же количество раз медленнее. Следовательно, период функции равен
Если две величины связаны между собой так, что с увеличением (уменьшением) значения одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз, то такие величины называются прямо пропорциональными.
О таких величинах говорят также, что они связаны между собой прямо пропорциональной зависимостью.
В природе и в окружающей нас жизни встречается множество подобных величин. Приведём примеры:
1. Время работы (день, два дня, три дня и т. д. ) и заработок, полученный за это время при подённой оплате труда.
2. Объём какого-нибудь предмета, сделанного из однородного материала, и вес этого предмета.
A) 1.7-0.3x=2+1.7x (переносим с буквой влево, свободные числа вправо) -0.3х-1.7х=2-1.7 -2х=0.3 -х=0.15 х=-0.15 Б)13х-14)-(15+6х)=-3х-3(приблизительно тоже самое, только еще и скобки раскрыть 13х-14-15-6х=-3х-3 13х-(-3х)-6х=-3-(-15)-(-14) 10х=26 х=5/13 В)3х+1=4 (Не знаю как жест, так напишу)(тут не сложно, просто число отрицательным не будет, т.к. под модулем 3х=4-1 3х=3 х=1 Г)5х+3(3х+7)=35(Тут так же раскрываем скобки, только еще с коэфицентом перед ними, т.е. умножим, то что в скобках 5х+9х+21=35 14х=14 х=1 Д)8х-(7х+8)=9(Думаю тут понятно, знаки местами меняются, из-за минуса перед скобкой. 8х-7х-8=9 х=17
4
Объяснение:
Наименьший положительный период функции
равен 1. При прибавлении или отнимании числа от аргумента график функции смещается влево или вправо вдоль оси абсцисс, таким образом это действие не оказывает влияния на длину периода. С умножением аргумента на коэффициент 
функция «пробегает» этот период в такое же количество раз медленнее. Следовательно, период функции 
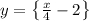равен 