Решение.
Сначала группируем слагаемые удобным образом, потом выносим общие множители. Затем пользуемся теоремой Виета для нахождения корней квадратного трёхчлена и раскладываем его на множители .
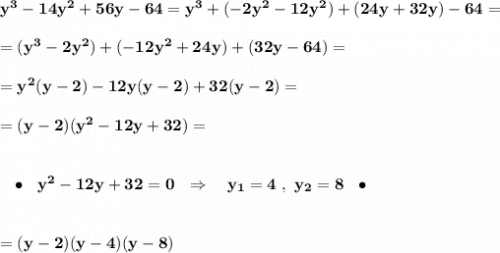
ответ: ниа.
объяснение:
к сожалению, не существует общего единого метода, следуя которому можно было бы решить любое уравнение, в котором участвуют тригонометрические функции. успех здесь могут обеспечить лишь хорошие знания формул и умение видеть те или иные полезные комбинации, что вырабатывается лишь практикой.
общая цель обычно состоит в преобразовании входящего в уравнение тригонометрического выражения к такому виду, чтобы корни находились из так называемых простейших уравнений:
сos px = a; sin gx = b; tg kx = c; ctg tx = d.
(y - 4)(y - 8)(y - 2).
Объяснение:
у³ - 14у² + 56у - 64 = (у³ - 64) + (- 14у² + 56у ) =
= у³ - 4³ - 14у•(у - 4) = (у - 4)(у² + 4у + 16) - 14у•(у - 4) =(у - 4)(у² + 4у + 16 - 14у) = (у - 4)(у² - 10у + 16 ) = (y - 4)(y² - 10y + 25 - 9) =
= (y - 4)•((y - 5)² - 3²) = (y - 4)(y - 5 - 3)(y - 5 + 3) = (y - 4)(y - 8)(y - 2).