Наименьший положительный корень
Объяснение:
Найти наименьший положительный корень уравнения
Раскроем скобки в правой части уравнения, для этого применим формулу сокращенного умножения
Так как по основному тригонометрическому тождеству
то получим
Найдем наименьший положительный корень.
1) При n = 1 получим положительный корень
2) При k=0 получим два корня , но положительным будет .
Наименьшим будем корень
#SPJ1
2x+3y=16 x=(16-3y)/2 x= (16-3y)/2 x=(16-3y)/2
{ { { {
3x-2y=11 3x-2y=11 (48-9y)/(2) - 2y=11 (48-9y-4y)/(2)=11
x=(16-3y)/2 x=(16-3y)/2 x=(16-3y)/2 x=(16-6)/2 x=10/2 x=5
{ { { { { {
(48-13y)/2=11 48-13y=22 26=13y y=2 y=2 y=2.
Наименьший положительный корень
Объяснение:
Найти наименьший положительный корень уравнения
Раскроем скобки в правой части уравнения, для этого применим формулу сокращенного умножения
Так как по основному тригонометрическому тождеству
то получим
Найдем наименьший положительный корень.
1) При n = 1 получим положительный корень
2) При k=0 получим два корня , но положительным будет
, но положительным будет 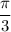 .
.
Наименьшим будем корень
#SPJ1