Дана система уравнений:
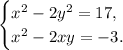
Из второго уравнения системы выразим  через
через  , получим:
, получим:
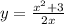 --------(1)
--------(1)
Поскольку 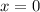 не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо
не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо  выражение (1), мы не потеряем решений системы:
выражение (1), мы не потеряем решений системы:
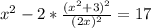 , отсюда
, отсюда
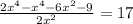 , отсюда
, отсюда
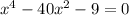 ---------(2)
---------(2)
Замена: пусть 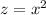 , тогда (2) примет вид:
, тогда (2) примет вид:
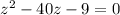 --------(3)
--------(3)
(3) - квадратное уравнение относительно 
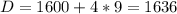
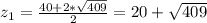
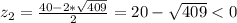
Но второй корень не удовлетворяет условию 
Возвращаясь к старой неизвестной, получим:
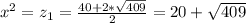 -------(4)
-------(4)
Из (4) получаем два значения  :
:
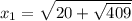
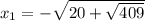
Подставим в первое уравнение системы вместо 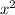 выражение (4), найдем соответствующие значения
выражение (4), найдем соответствующие значения  :
:
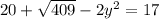 , отсюда
, отсюда
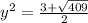 --------(5)
--------(5)
Из (5) получаем два значения  :
:
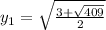
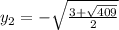
Итак, наша система имеет четыре решения:
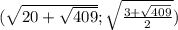
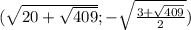
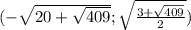
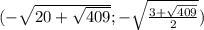
1)корень 2 sin 2x=1
sin2x= (корень из 2)/2
2x=(-1)^n*arcsin(корень 2/2)+пn, n принадлежит целым числам
x=(-1)^n*п/8+п/2*n, n принадлежит целым числам
ответ: (-1)^n*п/8+п/2*n, n принадлежит целым числам
2) sin(4x+п/8)=0
4x+п/8= пn, n принадлежит целым числам
4x=-п/8+пn, n принадлежит целым числам
x=-п/32+п/4*n, n принадлежит целым числам
ответ: -п/32+п/4*n, n принадлежит целым числам
3) sin (x/2 + п/3)-1=0
sin (x/2 + п/3)=1
x/2+п/3=п/2+2пn, n принадлежит целым числам
x/2=п/2 -п/3 + 2пn, n принадлежит целым числам
x=п- 2п/3 + 4пn, n принадлежит целым числам
х=п/3+4пn, n принадлежит целым числам
ответ: п/3+4пn, n принадлежит целым числам
4)sin(x-п/8)=-1
x-п/8=-п/2+2пn, n принадлежит целым числам
x= п/8-п/2+2пn, n принадлежит целым числам
x=-3п/2+2пn, n принадлежит целым числам
ответ: -3п/2+2пn, n принадлежит целым числам
5) cosx=-2, т.к. облсать значений функции cosx [-1;1], то данное уравнение не имеет решений.
а) Перепишем рівняння у вигляді (x²)² + 8x² - 9 = 0. Позначимо змінну x² = t. Отримаємо квадратне рівняння t² + 8t - 9 = 0. Розв'язуємо його за до формули коренів квадратного рівняння: t₁,₂ = (-8 ± √(8² + 4·1·9)) / (2·1) = (-8 ± √100) / 2 = -4 ± 5. Таким чином, маємо два значення t₁ = 1 та t₂ = -9. Повертаємось до змінної x²: x²₁ = 1, x²₂ = -9. Оскільки квадрат не може бути від'ємним числом, то розв'язками рівняння є x₁ = 1 та x₂ = -1.
б) Перепишемо рівняння у вигляді x√x + 7√x - 30 = 0. Позначимо змінну √x = t. Отримаємо квадратне рівняння t² + 7t - 30 = 0. Розв'язуємо його за до формули коренів квадратного рівняння: t₁,₂ = (-7 ± √(7² + 4·1·30)) / (2·1) = (-7 ± √169) / 2 = -3 або 10. Таким чином, маємо два значення √x₁ = -3 та √x₂ = 10. Оскільки корінь не може бути від'ємним числом, то розв'язком рівняння є x = 100.
в) Розкриваємо модуль: 2x - 9|x - 3| = 36|x + 3| або 2x - 9|x - 3| = -36|x + 3|. Розглянемо обидва випадки.
1) 2x - 9(x - 3) = 36(x + 3). Розв'язуємо це рівняння: 2x - 9x + 27 = 36x + 108, звідки x = -5.
2) 2x - 9(x - 3) = -36(x + 3). Розв'язуємо це рівняння: 2x - 9x + 27 = -36x - 108, звідки x = -3.
Отже, розв'язками рівняння є x₁ = -5 та x₂ = -3.